Segmenty proporcjonalne w trójkącie prostokątnym. Lekcja „proporcjonalne segmenty w trójkącie prostokątnym” Jak znaleźć proporcjonalne segmenty w trójkącie prostokątnym

Lekcja 40 b. a. h. C. p.n.e. H. ac. A. V. Wysokość trójkąta prostokątnego, narysowanego z wierzchołka kąta prostego, dzieli trójkąt na 2 podobne trójkąty prostokątne, z których każdy jest podobny do danego trójkąta. Znak podobieństwa trójkątów prostokątnych. Dwa trójkąty prostokątne są podobne, jeśli mają ten sam kąt ostry. Odcinek XY jest nazywany średnią proporcjonalną (średnią geometryczną) dla odcinków AB i CD, jeżeli Właściwość 1. Wysokość trójkąta prostokątnego wykreślonego z wierzchołka kąta prostego jest średnią proporcjonalną między rzutami nóg na przeciwprostokątną. Właściwość 2. Noga trójkąta prostokątnego jest średnią proporcjonalną między przeciwprostokątną a rzutem tej nogi na przeciwprostokątną.

Slajd 28 z prezentacji "Geometria "Podobne trójkąty"". Rozmiar archiwum z prezentacją to 232 KB.

Klasa geometrii 8

podsumowanie pozostałych prezentacji

"Rozwiązanie problemów z twierdzeniem Pitagorasa" - Trójkąt równoramienny ABC. Praktyczne zastosowanie twierdzenia Pitagorasa. ABCD jest czworobokiem. Powierzchnia kwadratu. Znajdź słońce. Dowód. Podstawy trapezu równoramiennego. Rozważ twierdzenie Pitagorasa. Powierzchnia czworoboku. Trójkąty prostokątne. Twierdzenie Pitagorasa. Kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg.

„Znalezienie obszaru równoległoboku” – Fundacja. Wzrost. Określanie wysokości równoległoboku. Znaki równości trójkątów prostokątnych. Obszar równoległoboku. Znajdź obszar trójkąta. Właściwości powierzchni. ćwiczenia ustne. Znajdź obszar równoległoboku. Wysokości równoległoboku. Znajdź obwód kwadratu. Obszar trójkąta. Znajdź obszar placu. Znajdź obszar prostokąta. Powierzchnia kwadratu.

„Kvadrat 8 klasa” - Czarny kwadrat. Zadania do pracy ustnej na całym obwodzie placu. Powierzchnia kwadratu. Znaki kwadratowe. Plac jest wśród nas. Kwadrat to prostokąt o równych wszystkich bokach. Kwadrat. Torba z kwadratową podstawą. zadania ustne. Ile kwadratów pokazano na obrazku. Właściwości kwadratowe. Bogaty kupiec. Zadania do pracy ustnej na terenie placu. Obwód kwadratu.

„Definicja symetrii osiowej” - Punkty leżące na tej samej prostopadłej. Narysuj dwie linie. Budowa. Punkty działki. Wskazówka. Figury, które nie mają symetrii osiowej. Sekcja. Brak współrzędnych. Postać. Kształty, które mają więcej niż dwie osie symetrii. Symetria. Symetria w poezji. Buduj trójkąty. Osie symetrii. Budowa segmentu. Budowanie punktu. Figury z dwiema osiami symetrii. Narody. Trójkąty. Proporcjonalność.

„Definiowanie podobnych trójkątów” — wielokąty. proporcjonalne cięcia. Stosunek pól podobnych trójkątów. Dwa trójkąty nazywane są podobnymi. Warunki. Skonstruuj trójkąt podając dwa kąty i dwusieczną w wierzchołku. Załóżmy, że musimy określić odległość do bieguna. Trzeci znak podobieństwa trójkątów. Zbudujmy trójkąt. ABC. Trójkąty ABC i ABC mają trzy równe boki. Określanie wysokości obiektu.

"Rozwiązanie twierdzenia Pitagorasa" - Części okien. Najprostszy dowód. Hammurabiego. Przekątna. Kompletny dowód. Dowód przez odejmowanie. Pitagorejczycy. Dowód metodą dekompozycji. Historia twierdzenia. Średnica. Dowód metodą dopełniacza. Dowód Epsteina. Kantor. Trójkąty. Obserwujący. Zastosowania twierdzenia Pitagorasa. Twierdzenie Pitagorasa. Stwierdzenie twierdzenia. Dowód Perygala. Zastosowanie twierdzenia.

Znak podobieństwa trójkątów prostokątnych

Przedstawmy najpierw znak podobieństwa trójkątów prostokątnych.

Twierdzenie 1

Znak podobieństwa trójkątów prostokątnych: dwa trójkąty prostokątne są podobne, jeśli mają po jednym równym kącie ostrym (ryc. 1).

Rysunek 1. Podobne trójkąty prawe

Dowód.

Załóżmy, że $\angle B=\angle B_1$. Ponieważ trójkąty są prostokątne, $\angle A=\angle A_1=(90)^0$. Dlatego są one podobne według pierwszego znaku podobieństwa trójkątów.

Twierdzenie zostało udowodnione.

Twierdzenie o wysokości w trójkącie prostokątnym

Twierdzenie 2

Wysokość trójkąta prostokątnego narysowanego z wierzchołka kąta prostego dzieli trójkąt na dwa podobne trójkąty prostokątne, z których każdy jest podobny do danego trójkąta.

Dowód.

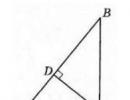
Daj nam trójkąt prostokątny $ABC$ o kącie prostym $C$. Narysuj wysokość $CD$ (rys. 2).

Rysunek 2. Ilustracja twierdzenia 2

Udowodnijmy, że trójkąty $ACD$ i $BCD$ są podobne do trójkąta $ABC$ oraz że trójkąty $ACD$ i $BCD$ są podobne.

Ponieważ $\angle ADC=(90)^0$, trójkąt $ACD$ jest prostokątny. Trójkąty $ACD$ i $ABC$ mają wspólny kąt $A$, dlatego zgodnie z Twierdzeniem 1 trójkąty $ACD$ i $ABC$ są podobne.

Ponieważ $\angle BDC=(90)^0$, trójkąt $BCD$ jest prostokątny. Trójkąty $BCD$ i $ABC$ mają wspólny kąt $B$, dlatego zgodnie z Twierdzeniem 1 trójkąty $BCD$ i $ABC$ są podobne.

Rozważmy teraz trójkąty $ACD$ i $BCD$

\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]

Dlatego, zgodnie z Twierdzeniem 1, trójkąty $ACD$ i $BCD$ są podobne.

Twierdzenie zostało udowodnione.

Średnia proporcjonalna

Twierdzenie 3

Wysokość trójkąta prostokątnego, wyciągnięta z wierzchołka kąta prostego, jest średnią proporcjonalną dla odcinków, na które wysokość dzieli przeciwprostokątną tego trójkąta.

Dowód.

Z Twierdzenia 2 mamy, że trójkąty $ACD$ i $BCD$ są podobne, zatem

Twierdzenie zostało udowodnione.

Twierdzenie 4

Noga trójkąta prostokątnego jest średnią proporcjonalną między przeciwprostokątną i odcinkiem przeciwprostokątnej ujętym między nogę a wysokością wyprowadzoną z wierzchołka kąta.

Dowód.

W dowodzie twierdzenia użyjemy notacji z rysunku 2.

Z Twierdzenia 2 mamy, że trójkąty $ACD$ i $ABC$ są podobne, stąd

Twierdzenie zostało udowodnione.

Znak podobieństwa trójkątów prostokątnych

Przedstawmy najpierw znak podobieństwa trójkątów prostokątnych.

Twierdzenie 1

Znak podobieństwa trójkątów prostokątnych: dwa trójkąty prostokątne są podobne, jeśli mają po jednym równym kącie ostrym (ryc. 1).

Rysunek 1. Podobne trójkąty prawe

Dowód.

Załóżmy, że $\angle B=\angle B_1$. Ponieważ trójkąty są prostokątne, $\angle A=\angle A_1=(90)^0$. Dlatego są one podobne według pierwszego znaku podobieństwa trójkątów.

Twierdzenie zostało udowodnione.

Twierdzenie o wysokości w trójkącie prostokątnym

Twierdzenie 2

Wysokość trójkąta prostokątnego narysowanego z wierzchołka kąta prostego dzieli trójkąt na dwa podobne trójkąty prostokątne, z których każdy jest podobny do danego trójkąta.

Dowód.

Daj nam trójkąt prostokątny $ABC$ o kącie prostym $C$. Narysuj wysokość $CD$ (rys. 2).

Rysunek 2. Ilustracja twierdzenia 2

Udowodnijmy, że trójkąty $ACD$ i $BCD$ są podobne do trójkąta $ABC$ oraz że trójkąty $ACD$ i $BCD$ są podobne.

Ponieważ $\angle ADC=(90)^0$, trójkąt $ACD$ jest prostokątny. Trójkąty $ACD$ i $ABC$ mają wspólny kąt $A$, dlatego zgodnie z Twierdzeniem 1 trójkąty $ACD$ i $ABC$ są podobne.

Ponieważ $\angle BDC=(90)^0$, trójkąt $BCD$ jest prostokątny. Trójkąty $BCD$ i $ABC$ mają wspólny kąt $B$, dlatego zgodnie z Twierdzeniem 1 trójkąty $BCD$ i $ABC$ są podobne.

Rozważmy teraz trójkąty $ACD$ i $BCD$

\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]

Dlatego, zgodnie z Twierdzeniem 1, trójkąty $ACD$ i $BCD$ są podobne.

Twierdzenie zostało udowodnione.

Średnia proporcjonalna

Twierdzenie 3

Wysokość trójkąta prostokątnego, wyciągnięta z wierzchołka kąta prostego, jest średnią proporcjonalną dla odcinków, na które wysokość dzieli przeciwprostokątną tego trójkąta.

Dowód.

Z Twierdzenia 2 mamy, że trójkąty $ACD$ i $BCD$ są podobne, zatem

Twierdzenie zostało udowodnione.

Twierdzenie 4

Noga trójkąta prostokątnego jest średnią proporcjonalną między przeciwprostokątną i odcinkiem przeciwprostokątnej ujętym między nogę a wysokością wyprowadzoną z wierzchołka kąta.

Dowód.

W dowodzie twierdzenia użyjemy notacji z rysunku 2.

Z Twierdzenia 2 mamy, że trójkąty $ACD$ i $ABC$ są podobne, stąd

Twierdzenie zostało udowodnione.

Cele Lekcji:

wprowadzić pojęcie średniej proporcjonalnej (średniej geometrycznej) dwóch odcinków;
rozważ problem proporcjonalnych odcinków w trójkącie prostokątnym: właściwość wysokości trójkąta prostokątnego narysowanego z wierzchołka kąta prostego;
kształtowanie umiejętności wykorzystania studiowanego tematu w procesie rozwiązywania problemów.

Rodzaj lekcji: lekcja uczenia się nowego materiału.

Plan:

Moment organizacyjny.
Aktualizacja wiedzy.
Badanie właściwości wysokości trójkąta prostokątnego narysowanego z wierzchołka pod kątem prostym:
- etap przygotowawczy;
- wprowadzanie;
- asymilacja.
Wprowadzenie pojęcia średniej proporcjonalnej do dwóch odcinków.
Przyswojenie pojęcia średniej proporcji dwóch segmentów.
Dowód konsekwencji:
- wysokość trójkąta prostokątnego, wyciągniętego z wierzchołka kąta prostego, jest średnią proporcjonalną między segmentami, na które podzielona jest przeciwprostokątna przez tę wysokość;
- noga trójkąta prostokątnego to średnia proporcjonalna między przeciwprostokątną a odcinkiem przeciwprostokątnej zawartą między nogą a wzrostem.
Rozwiązywanie problemów.
Zreasumowanie.
Zadawanie pracy domowej.

Podczas zajęć

I. ORGANIZACJA

Cześć chłopaki, usiądźcie. Czy wszyscy są gotowi na lekcję?

Rozpoczynamy pracę.

II. AKTUALIZACJA WIEDZY

Jakiego ważnego pojęcia matematycznego nauczyłeś się na poprzednich lekcjach? ( z pojęciem podobieństwa trójkąta)

- Pamiętajmy, które dwa trójkąty nazywamy podobnymi? (dwa trójkąty są nazywane podobnymi jeśli ich kąty są odpowiednio równe a boki jednego trójkąta są proporcjonalne do podobnych boków drugiego trójkąta)

Czego używamy, aby udowodnić podobieństwo dwóch trójkątów? (

- Wymień te znaki. (sformułuj trzy znaki podobieństwa trójkątów)

III. BADANIE WŁAŚCIWOŚCI WYSOKOŚCI TRÓJKĄTA PROSTOKĄTNEGO REALIZOWANEGO Z WIERZCHODU KĄTA PROSTEGO

a) etap przygotowawczy

- Chłopaki, spójrzcie na pierwszy slajd. ( załącznik) Oto dwa trójkąty prostokątne - i . i są odpowiednio wysokościami i. .

Zadanie 1. a) Określ, czy i są podobne.

Czego używamy, aby udowodnić podobieństwo trójkątów? ( oznaki podobieństwa trójkątów)

(pierwszy znak, ponieważ nic nie wiadomo o bokach trójkątów w zadaniu)

. (Dwie pary: 1. ∟B= ∟B1 (linie proste), 2. ∟A= ∟A 1)

- Wyciągnij wniosek. ( przez pierwszy znak podobieństwa trójkątów ~)

Zadanie 1. b) Określ, czy i są podobne.

Jakie kryterium podobieństwa zastosujemy i dlaczego? (pierwszy znak, bo w zadaniu nic nie wiadomo o bokach trójkątów))

Ile par równych kątów musimy znaleźć? Znajdź te pary (ponieważ trójkąty są prostokątne, wystarczy jedna para równych kątów: ∟A= ∟A 1)

- Podejdź do konkluzji. (po pierwszym znaku podobieństwa trójkątów wnioskujemy, że te trójkąty są podobne).

W wyniku rozmowy slajd 1 wygląda tak:

b) odkrycie twierdzenia

Zadanie 2.

Określ, czy i i są podobne. W wyniku rozmowy budowane są odpowiedzi, które znajdują odzwierciedlenie na slajdzie.

- Cyfra wskazywała, że . Czy używaliśmy tej miary stopnia odpowiadając na pytania zadań? ( Nie, nie używany)

- Chłopaki, wyciągnijcie wniosek: na jakie trójkąty wysokość wyciągnięta z wierzchołka pod kątem prostym dzieli trójkąt prawy? (podsumuj)

- Powstaje pytanie: czy te dwa trójkąty prostokątne, na które wysokość dzieli trójkąt prostokątny, będą do siebie podobne? Spróbujmy znaleźć pary równych kątów.

W wyniku rozmowy powstaje zapis:

- A teraz zróbmy pełny wniosek. ( WNIOSEK: wysokość trójkąta prostokątnego wyciągniętego z wierzchołka kąta prostego dzieli trójkąt na dwa podobny

- To. sformułowaliśmy i udowodniliśmy twierdzenie o własności wysokości trójkąta prostokątnego.

Ustalmy strukturę twierdzenia i zróbmy rysunek. Co podano w twierdzeniu i co należy udowodnić? Uczniowie zapisują w swoich zeszytach:

Udowodnijmy pierwszy punkt twierdzenia dla nowego rysunku. Jakie kryterium podobieństwa zastosujemy i dlaczego? (Po pierwsze, ponieważ nic nie wiadomo o bokach trójkątów w twierdzeniu)

Ile par równych kątów musimy znaleźć? Znajdź te pary. (W tym przypadku wystarczy jedna para: ∟A-ogólnie)

- Podejdź do konkluzji. Trójkąty są podobne. W rezultacie pokazano przykład sformułowania twierdzenia

- Drugi i trzeci punkt napisz sam w domu.

c) asymilacja twierdzenia

- Więc sformułuj twierdzenie jeszcze raz (Wysokość trójkąta prostokątnego, narysowanego z wierzchołka kąta prostego, dzieli trójkąt na dwa podobny trójkąty prostokątne, z których każdy jest podobny do tego)

- Ile par trójkątów podobnych w konstrukcji "w trójkącie prostokątnym wysokość od wierzchołka kąta prostego" można znaleźć według tego twierdzenia? ( Trzy pary)

Uczniowie otrzymują następujące zadanie:

IV. WPROWADZENIE KONCEPCJI ŚREDNIEJ PROPORCJONALNOŚCI DWÓCH LINII

Teraz poznamy nową koncepcję.

Uwaga!

Definicja. Sekcja XY nazywa średnia proporcjonalna (Średnia geometryczna) między segmentami AB oraz płyta CD, Jeśli

(napisz w notatniku).

V. POWIĄZANIE KONCEPCJI ŚREDNIEJ PROPORCJONALNOŚCI DWÓCH LINII

Przejdźmy teraz do następnego slajdu.

Ćwiczenie 1. Znajdź długość średnich proporcjonalnych odcinków MN i KP, jeśli MN = 9 cm, KP = 16 cm.

- Co jest podane w zadaniu? ( Dwa segmenty i ich długości: MN = 9 cm, KP = 16 cm)

- Co potrzebujesz znaleźć? ( Długość średniej proporcjonalnej tych segmentów)

- Jaki jest wzór na średnią proporcjonalną i jak ją znaleźć?

(Wstawiamy dane do wzoru i znajdujemy długość średniej podpory.)

Zadanie nr 2. Znajdź długość odcinka AB, jeśli średnia proporcja odcinków AB i CD wynosi 90 cm i CD = 100 cm

- Co jest podane w zadaniu? (długość odcinka CD = 100 cm a średnia proporcja odcinków AB i CD wynosi 90 cm)

Co powinno znaleźć się w problemie? ( Długość odcinka AB)

- Jak zamierzamy rozwiązać ten problem? (Zapiszmy wzór na przeciętne proporcjonalne odcinki AB i CD, wyrażmy z niego długość AB i zastąpmy danymi problemu.)

VI. WNIOSEK

- Dobra robota chłopcy. A teraz wróćmy do podobieństwa trójkątów, udowodnionego przez nas w twierdzeniu. Powtórz twierdzenie. ( Wysokość trójkąta prostokątnego narysowanego z wierzchołka kąta prostego dzieli trójkąt na dwa podobny trójkąty prostokątne, z których każdy jest podobny do danego)

- Najpierw użyjmy podobieństwa trójkątów i . Co z tego wynika? ( Z definicji podobieństwa boki są proporcjonalne do boków podobnych)

- Jaka równość zostanie osiągnięta przy użyciu podstawowej właściwości proporcji? ()

– Ekspresuj CD i wyciągaj wnioski (;.

Wniosek: wysokość trójkąta prostokątnego, wyciągniętego z wierzchołka kąta prostego, jest średnią proporcjonalną między segmentami, na które podzielona jest przeciwprostokątna przez tę wysokość)

- A teraz udowodnij sobie, że noga trójkąta prostokątnego jest średnią proporcjonalną między przeciwprostokątną a odcinkiem przeciwprostokątnej zawartym między nogą a wysokością. Znajdujemy od - ... odcinków, na które dzieli się przeciwprostokątną przez ta wysokość )

Noga trójkąta prostokątnego jest średnią proporcjonalną między ... (- ... przeciwprostokątna i odcinek przeciwprostokątnej zamknięte między tą nogą a wzrostem )

– Gdzie stosujemy wyuczone stwierdzenia? ( Podczas rozwiązywania problemów)

IX. USTAWIANIE PRACY DOMOWEJ

d/z: nr 571, nr 572 (a, e), samodzielna praca w zeszycie, teoria.

Dziś Państwa uwagę zapraszam na kolejną prezentację na niesamowity i tajemniczy temat - geometrię. W tej prezentacji przedstawimy nową właściwość kształtów geometrycznych, w szczególności koncepcję segmentów proporcjonalnych w trójkątach prostokątnych.

Najpierw musisz pamiętać, co to jest trójkąt? Jest to najprostszy wielokąt składający się z trzech wierzchołków połączonych trzema segmentami. Trójkąt prostokątny to trójkąt, w którym jeden z kątów wynosi 90 stopni. Zapoznałeś się już z nimi bardziej szczegółowo w naszych poprzednich materiałach szkoleniowych przedstawionych Twojej uwadze.

Wracając więc do naszego dzisiejszego tematu, oznaczamy, że wysokość trójkąta prostokątnego narysowanego pod kątem 90 stopni dzieli go na dwa trójkąty, które są podobne zarówno do siebie, jak i do pierwotnego. Wszystkie interesujące Cię rysunki i wykresy znajdują się w proponowanej prezentacji i zalecamy się do nich odnieść wraz z opisywanym wyjaśnieniem.

Graficzny przykład powyższej tezy można zobaczyć na drugim slajdzie. Trójkąty są podobne, ponieważ mają dwa identyczne kąty. Jeśli określisz bardziej szczegółowo, wysokość obniżona do przeciwprostokątnej tworzy z nią kąt prosty, to znaczy, że istnieją już identyczne kąty, a każdy z utworzonych kątów ma również jeden wspólny kąt jako swój pierwotny. Wynikiem są dwa równe sobie kąty. Oznacza to, że trójkąty są podobne.

Zaznaczmy także, co samo w sobie oznacza pojęcie „średnia proporcjonalna” lub „średnia geometryczna”? Jest to pewien odcinek XY dla odcinków AB i CD, gdy jest równy pierwiastkowi kwadratowemu z iloczynu ich długości.

Z czego wynika również, że noga trójkąta prostokątnego jest średnią geometryczną między przeciwprostokątną a rzutem tej nogi na przeciwprostokątną, czyli na drugą nogę.

Inną właściwością trójkąta prostokątnego jest to, że jego wysokość, narysowana pod kątem 90o, jest średnią proporcjonalną między rzutami nóg na przeciwprostokątną. Jeśli odwołasz się do prezentacji i innych materiałów, na które zwróciłeś uwagę, zobaczysz, że istnieje dowód tej tezy w bardzo prostej i przystępnej formie. Wcześniej udowodniliśmy już, że powstałe trójkąty są podobne do siebie i do pierwotnego trójkąta. Następnie, korzystając ze stosunku nóg tych figur geometrycznych, dochodzimy do wniosku, że wysokość trójkąta prostokątnego jest wprost proporcjonalna do pierwiastka kwadratowego iloczynu odcinków, które powstały w wyniku obniżenia wysokości z kąt prosty pierwotnego trójkąta.

Ostatnią rzeczą w prezentacji jest to, że ramię trójkąta prostokątnego jest średnią geometryczną dla przeciwprostokątnej i jej odcinka znajdującego się między ramieniem a wysokością narysowaną pod kątem równym 90 stopni. Ten przypadek należy rozpatrywać z tej strony, że te trójkąty są do siebie podobne, a odnogę jednego z nich uzyskuje się przeciwprostokątną drugiego. Ale poznasz to bardziej szczegółowo, studiując proponowane materiały.