Algoritmus jednoduchej metódy. Jednoduchá metóda na riešenie zlp. Podmienene štandardný problém lineárneho programovania

Ak potrebujete vyriešiť problém s lineárnym programovaním pomocou simplexových tabuliek, naša online služba vám bude veľkou pomocou. Metóda simplex znamená sekvenčné vyčíslenie všetkých vrcholov rozsahu prípustných hodnôt s cieľom nájsť vrchol, kde funkcia nadobúda extrémnu hodnotu. V prvej fáze sa nájde nejaké riešenie, ktoré sa zlepšuje v každom nasledujúcom kroku. Toto riešenie sa nazýva základné. Tu je postupnosť akcií pri riešení problému s lineárnym programovaním pomocou simplexovej metódy:

Prvý krok. V zostavenej tabuľke sa musíte najskôr pozrieť na stĺpec s voľnými členmi. Ak sú v ňom negatívne prvky, potom je potrebné pristúpiť k druhému kroku, ak nie, potom k piatemu.

Druhý krok. V druhom kroku je potrebné rozhodnúť, ktorú premennú vylúčiť zo základu a ktorú zahrnúť, aby sa prepočítal simplexovú tabuľku. Za týmto účelom sa pozrite do stĺpca s voľnými členmi a nájdite v ňom negatívny prvok. Riadok s negatívnym prvkom sa bude nazývať úvodná čiara. V ňom nájdeme maximálny negatívny prvok v absolútnej hodnote, zodpovedajúci stĺpec - sledovateľ. Ak sú medzi voľnými členmi záporné hodnoty, ale nie v zodpovedajúcom riadku, potom takáto tabuľka nebude mať žiadne riešenia. Zmenou v úvodnom riadku je ten v stĺpci voľných členov vylúčený zo základu a do základu je zahrnutá premenná zodpovedajúca vedúcemu stĺpcu.

Stôl 1.

základné premenné	Slobodní členovia v obmedzeniach	Nezákladné premenné
základné premenné	Slobodní členovia v obmedzeniach	x 1	x 2	...	x l	...	x n
x n + 1	b 1	a 11	a 12	...	1l	...	a 1n
x n + 2	b 2	a 21	a 22	...	2l	...	2n
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n + r	b2	a r1	a r2	...	rl	...	rn
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n + m	b m	a m1	m2	...	ml	...	a mn
F (x) max	F 0	-c 1	-c 2	...	-c 1	...	-c n

Krok tri. V treťom kroku prepočítame celú simplexovú tabuľku pomocou špeciálnych vzorcov, tieto vzorce je možné vidieť pomocou.

Štvrtý krok. Ak po prepočte zostanú negatívne prvky v stĺpci voľných výrazov, prejdite na prvý krok, ak žiadne neexistujú, potom na piaty.

Piaty krok. Ak ste dosiahli piaty krok, našli ste riešenie, ktoré je prijateľné. To však neznamená, že je optimálny. Optimálne to bude iba vtedy, ak sú všetky prvky v rade F kladné. Ak to tak nie je, je potrebné vylepšiť riešenie, pre ktoré podľa nasledujúceho algoritmu nájdeme vedúci riadok a stĺpec pre nasledujúci prepočet. Na začiatku nájdeme v riadku F minimálne záporné číslo, pričom hodnotu funkcie nepočítame. Stĺpec s týmto číslom bude vedúcim. Aby sme našli vedúci riadok, nájdeme pomer zodpovedajúceho voľného člena a prvku z úvodného stĺpca za predpokladu, že sú kladné. Minimálny vzťah vám umožní určiť vedúci riadok. Tabuľku prepočítame opäť pomocou vzorcov, t.j. prejdite na krok 3.

Tu je manuálne (nie apletové) riešenie dvoch problémov simplexovou metódou (podobné riešeniu pomocou apletu) s podrobnými vysvetleniami, aby ste porozumeli algoritmu na riešenie problémov simplexovou metódou. Prvý problém obsahuje znaky nerovnosti iba „≤“ (problém s počiatočným základom), druhý môže obsahovať znaky „≥“, „≤“ alebo „=“ (problém s umelým základom), riešia sa rôznymi spôsobmi .

Jednoduchá metóda, riešenie problému s počiatočným základom

1)Jednoduchá metóda pre problém s počiatočným základom (všetky znaky obmedzení nerovnosti „≤“).

Zapíšeme úlohu do kanonický forma, t.j. obmedzenia nerovnosti je možné prepísať ako rovnosti pridaním súvaha premenné:

Tento systém je systém so základom (základ s 1, s 2, s 3, každý z nich je zahrnutý iba v jednej rovnici systému s koeficientom 1), x 1 a x 2 sú voľné premenné. Problémy, pri riešení ktorých sa používa simplexová metóda, musia mať tieto dve vlastnosti: - sústava obmedzení musí byť sústavou rovníc so základom; - voľné termíny všetkých rovníc v systéme musia byť nezáporné.

Výsledný systém je systém na základe a jeho bezplatné podmienky sú nezáporné; preto môžeme podať žiadosť simplexová metóda... Zostavme prvú simplexovú tabuľku (iterácia 0), na ktorej je problém vyriešený simplexová metóda, t.j. tabuľka koeficientov objektívnej funkcie a sústava rovníc pre zodpovedajúce premenné. Tu „BP“ znamená stĺpec základných premenných, „Riešenie“ - stĺpec pravých strán rovníc systému. Riešenie nie je optimálne, pretože v riadku z sú negatívne koeficienty.

iterácia metódy simplex 0

							Postoj

Aby sme vylepšili riešenie, prejdeme k ďalšej iterácii simplexová metóda, dostaneme nasledujúcu simplexnú tabuľku. Ak to chcete urobiť, musíte si vybrať permisívny stĺpček, t.j. premenná, ktorá bude zahrnutá do základu pri ďalšej iterácii simplexovej metódy. Je vybraný najväčším záporným koeficientom v absolútnej hodnote v z -riadku (pri maximálnom probléme) -v počiatočnej iterácii simplexovej metódy je to stĺpec x 2 (koeficient -6).

Potom sa vyberie permisívna struna, t.j. premenná, ktorá opustí základ pri ďalšej iterácii simplexovej metódy. Je vybraný najmenším pomerom stĺpca „Rozhodnutie“ k zodpovedajúcim pozitívnym prvkom rozlišovacieho stĺpca (stĺpček „Pomer“) - v počiatočnej iterácii je to riadok s 3 (koeficient 20).

Povolený prvok je na priesečníku rozlišovacieho stĺpca a rozlišovacieho riadku, jeho bunka je zvýraznená, rovná sa 1. Preto pri ďalšej iterácii simplexovej metódy nahradí premenná x 2 v základe s 1. Všimnite si toho, že vzťah nie je hľadaný v riadku z, ale je tam vložená pomlčka „-“. Ak existujú rovnaké minimálne vzťahy, vyberie sa ktorýkoľvek z nich. Ak sú v stĺpci rozlíšenia všetky koeficienty menšie alebo rovné 0, potom je riešenie problému nekonečné.

Vyplnime nasledujúcu tabuľku „Iterácia 1“. Získame to z tabuľky „Iterácia 0“. Cieľom ďalších transformácií je zmeniť rozlišovací stĺpec x 2 na jeden (s jedným namiesto rozlišovacieho prvku a nulami namiesto ostatných prvkov).

1) Výpočet riadku x 2 tabuľky „Iterácia 1“. Najprv rozdelíme všetky členy rozlišovacieho riadku s 3 tabuľky "Iterácia 0" na rozlišovací prvok (v tomto prípade sa rovná 1) tejto tabuľky, v tabuľke Iterácie 1 získame riadok x 2. Pretože rozlišovací prvok je v tomto prípade rovný 1, potom sa riadok s 3 tabuľky „Iterácia 0“ bude zhodovať s riadkom x 2 tabuľky „Iterácia 1“. Dostali sme riadok x 2 tabuľky „Iterácia 1“ 0 1 0 0 1 20, zvyšok riadkov tabuľky „Iterácia 1“ sa získa z tohto riadka a riadkov tabuľky „Iterácia 0“ takto:

2) Výpočet z-riadka tabuľky „Iterácia 1“. Namiesto -6 v prvom riadku (riadok z) v stĺpci x 2 tabuľky Iterácie 0 by malo byť 0 v prvom riadku tabuľky Iterácie 1. Za týmto účelom vynásobíme všetky prvky riadku x 2 tabuľky „Iterácia 1“ 0 1 0 0 1 20 číslom 6, dostaneme 0 6 0 0 6 120 a tento riadok pripočítame k prvému riadku (z - riadok) tabuľka „Iterácia 0“ -4 -6 0 0 0 0, dostaneme -4 0 0 0 6 120. V stĺpci x 2 sa objavila nula 0, cieľ bol dosiahnutý. Povolené prvky stĺpca x 2 sú zvýraznené červenou farbou.

3) Výpočet riadku s 1 tabuľky „Iterácia 1“. Na mieste 1 v s 1 riadku tabuľky „Iterácia 0“ musí byť v tabuľke „Iterácia 1“ 0. Za týmto účelom vynásobíme všetky prvky riadku x 2 tabuľky „Iterácia 1“ 0 1 0 0 1 20 číslom -1, dostaneme 0 -1 0 0 -1 –20 a tento riadok pridáme s s 1 - riadok tabuľky „Iterácia 0“ 2 1 1 0 0 64, dostaneme riadok 2 0 1 0 -1 44. V stĺpci x 2 dostaneme požadovanú 0.

4) Výpočet riadku s 2 tabuľky „Iterácia 1“. Na mieste 3 v s 2 riadku tabuľky „Iterácia 0“ musí byť v tabuľke „Iterácia 1“ 0. Za týmto účelom vynásobíme všetky prvky riadku x 2 tabuľky „Iterácia 1“ 0 1 0 0 1 20 číslom -3, dostaneme 0 -3 0 0 -3 -60 a tento riadok pridáme s s 1 - riadok tabuľky „Iterácia 0“ 1 3 0 1 0 72, dostaneme riadok 1 0 0 1 -3 12. V stĺpci x 2 sa získa požadovaná 0. Stĺpec x 2 v tabuľke „Iterácia 1“ má staň sa jedným, obsahuje jeden 1 a zvyšok 0.

Riadky tabuľky „Iterácia 1“ sa získajú podľa nasledujúceho pravidla:

Nový riadok = starý riadok - (faktor stĺpca rozlíšenia starého riadka) * (nový riadok rozlíšenia).

Napríklad pre z-riadok máme:

Starý riadok z (-4 -6 0 0 0 0) -( -6) * Nový rozlišovací riadok -(0 -6 0 0 -6 -120) = Nový riadok z (-4 0 0 0 6 120).

Pri nasledujúcich tabuľkách sa prepočítavanie prvkov tabuľky robí rovnako, preto to vynechávame.

iterácia metódy simplex 1

							Postoj

Ak povolíme stĺpec x 1, riešenie riadkov s 2, s 2, opustíme základ, x 1 zadáme základ. Presne rovnakým spôsobom získame zvyšok simplexových tabuliek, kým nedostaneme tabuľku so všetkými kladnými koeficientmi v riadku z. Toto je znak optimálnej tabuľky.

iterácia simplexovej metódy 2

							Postoj

Rozlišovací stĺpec s 3, rozlišovací riadok s 1, s 1 opúšťa základ, s 3 vstupuje do základu.

iterácia simplexovej metódy 3

							Postoj

V rade z sú všetky koeficienty nezáporné, preto je optimálne riešenie x 1 = 24, x 2 = 16, z max = 192.

Lineárne programovanie je metóda matematického modelovania navrhnutá tak, aby optimalizovala používanie obmedzených zdrojov. Droga sa úspešne používa v armáde, priemysle, poľnohospodárstve, doprave, ekonomike, zdravotníctve a dokonca aj v sociálnych vedách. Rozšírené používanie tejto metódy podporujú aj vysoko účinné počítačové algoritmy, ktoré túto metódu implementujú. Optimalizačné algoritmy pre ďalšie, komplexnejšie typy problémov modelov a operačného výskumu (IO) vrátane celočíselného, nelineárneho a stochastického programovania sú založené na algoritmoch lineárneho programovania.

Úloha optimalizácie Ide o ekonomický a matematický problém, ktorý spočíva v nájdení optimálnej (maximálnej alebo minimálnej) hodnoty objektívnej funkcie a hodnoty premenných musia patriť do určitého rozsahu prípustných hodnôt.

V najvšeobecnejšej podobe je problém lineárneho programovania matematicky zapísaný takto:

kde X = (x 1 , X 2 , ..., X n ) ; W- rozsah prípustných hodnôt premenných X 1 , X 2 , ..., X n ;f (X)- objektívna funkcia.

Na vyriešenie problému s optimalizáciou stačí nájsť jeho optimálne riešenie, t.j. označte to tak pre hocikoho.

Problém optimalizácie je neriešiteľný, ak nemá optimálne riešenie. Najmä problém maximalizácie bude neriešiteľný, ak objektívna funkcia f (X) nie je obmedzený vyššie na prípustnú množinu W.

Metódy riešenia problémov s optimalizáciou závisia od typu objektívnej funkcie f (X), a o štruktúre prípustnej množiny W... Ak je objektívna funkcia v probléme funkcia n premenné, potom sa metódy riešenia nazývajú metódy matematického programovania.

Charakteristické vlastnosti problémov s lineárnym programovaním sú nasledujúce:

ukazovateľ optimality f (X) je lineárna funkcia prvkov riešenia X = (x 1 , X 2 , ..., X n ) ;

reštriktívne podmienky uložené na možné riešenia majú formu lineárnych rovností alebo nerovností.

Problém s lineárnym programovaním nazýva sa úloha operačného výskumu, ktorého matematický model má formu:

(2) (3) (4) (5)

V tomto prípade ide o sústavu lineárnych rovníc (3) a nerovností (4), (5), ktorá určuje prípustný súbor riešení problému. W sa volá systém obmedzení problémy lineárneho programovania a lineárna funkcia f (X) zavolal cieľová funkcia alebo kritérium optimality .

Platné riešenie Je zbierka čísel ( plán ) X = (X 1 , X 2 , ... , X n ) uspokojenie obmedzení problému. Optimálne riešenie Je plán, v ktorom objektívna funkcia nadobúda svoju maximálnu (minimálnu) hodnotu.

Ak má matematický model problému s lineárnym programovaním tvar:

potom hovoria, že problém je prezentovaný v kanonická forma .

Akýkoľvek problém s lineárnym programovaním je možné zredukovať na problém lineárneho programovania v kanonickej forme. Aby ste to urobili, vo všeobecnom prípade musíte byť schopní zredukovať problém maximalizácie na problém minimalizácie; prejsť od obmedzení nerovnosti k obmedzeniam rovnosti a nahradiť premenné, ktoré nedodržiavajú podmienku non-negativity. Maximalizácia nejakej funkcie je ekvivalentná minimalizácii tej istej funkcie s opačným znamienkom a naopak.

Pravidlo na zníženie problému s lineárnym programovaním na kanonickú formu je nasledujúce:

ak je v pôvodnom probléme potrebné určiť maximum lineárnej funkcie, mali by ste zmeniť znamienko a hľadať minimum tejto funkcie;

ak je pravá strana obmedzení záporná, potom by sa toto obmedzenie malo vynásobiť -1;

ak medzi obmedzeniami existujú nerovnosti, potom sa zavedením ďalších nezáporných premenných transformujú na rovnosti;

ak nejaká premenná X j nemá žiadne znamienkové obmedzenia, potom je nahradený (v objektívnej funkcii a vo všetkých obmedzeniach) rozdielom medzi dvoma novými nezápornými premennými: X 3 = x 3 + - X 3 - , kde X 3 + , X 3 - ≥ 0 .

Príklad 1... Redukcia problému s lineárnym programovaním na kanonickú formu:

min. L = 2x 1 + x 2 - X 3 ; 2x 2 - X 3 ≤ 5; X 1 + x 2 - X 3 ≥ -1; 2x 1 - X 2 ≤ -3; X 1 ≤ 0; X 2 ≥ 0; X 3 ≥ 0.

Do každej rovnice systému obmedzení zavedieme premenné nivelizácie X 4 , X 5 , X 6 ... Systém bude zapísaný vo forme rovností a v prvej a tretej rovnici systému obmedzení premenné X 4 , X 6 sa zadávajú na ľavej strane so znamienkom „+“ a v druhej rovnici premenná X 5 zadané znakom „-“.

2x 2 - X 3 + x 4 = 5; X 1 + x 2 - X 3 - X 5 = -1; 2x 1 - X 2 + x 6 = -3; X 4 ≥ 0; X 5 ≥ 0; X 6 ≥ 0.

Voľné výrazy v kanonickej forme musia byť kladné, preto vynásobíme posledné dve rovnice -1:

2x 2 - X 3 + x 4 = 5; -X 1 - X 2 + x 3 + x 5 = 1; -2x 1 + x 2 - X 6 = 3.

Jednoduchá metóda na riešenie problémov s lineárnym programovaním.

Algoritmus simplexovej metódy nájde optimálne riešenie zvážením obmedzeného počtu prípustných základných riešení. Algoritmus simplexovej metódy vždy začína nejakým uskutočniteľným základným riešením a potom sa pokúša nájsť ďalšie uskutočniteľné základné riešenie, ktoré „zlepšuje“ hodnotu objektívnej funkcie. To je možné iba vtedy, ak zvýšenie akejkoľvek nulovej (nebázickej) premennej vedie k zlepšeniu hodnoty objektívnej funkcie. Ale aby sa nebázická premenná stala kladnou, musí byť jedna zo súčasných základných premenných nula, t.j. previesť na non-basic. To je nevyhnutné, aby nové riešenie presne obsahovalo m základné premenné. V súlade s terminológiou simplexovej metódy sa zvolená nulová premenná nazýva predstavený (k základu), a odstránená základná premenná je vylúčené (zo základu).

Budú sa volať dve pravidlá pre výber zavedených a vylučujúcich premenných v simplexovej metóde podmienka optimality a podmienka prípustnosti ... Sformulujme tieto pravidlá a zvážme aj postupnosť akcií vykonaných pri implementácii simplexovej metódy.

Podmienka optimality. Premenná zavedená v probléme maximalizácie (minimalizácie) je nebázická premenná majúca najväčší negatívny (pozitívny) koeficient v cieľ-reťazec. Ak v cieľ-reťazec má niekoľko takýchto koeficientov, potom sa výber vstupnej premennej robí ľubovoľne. Optimálne riešenie sa dosiahne, keď sa v cieľ-reťazec, všetky koeficienty nebázických premenných budú nezáporné (kladné).

Podmienka prípustnosti. V probléme maximalizácie aj v probléme minimalizácie je základná premenná zvolená ako vylúčená, pre ktorú je pomer hodnoty pravej strany obmedzenia k kladnému koeficientu úvodného stĺpca minimálny. Ak existuje niekoľko základných premenných s touto vlastnosťou, potom sa voľba vylúčenej premennej vykoná ľubovoľne.

Predstavme si algoritmus na riešenie problému s lineárnym programovaním na nájdenie maxima pomocou simplexových tabuliek.

F = s 1 x 1 + s 2 x 2 +… + s n x n max

x 1 0, x 2 0, ..., x n 0.

1. krok... Zavedieme ďalšie premenné a výsledný systém rovníc a lineárnu funkciu napíšeme vo forme rozšíreného systému.

F -c 1 x 1 –c 2 x 2 -… –c n x n = 0 = c p.

2. krok. Zostavenie počiatočnej simplexovej tabuľky.

Premenné	Základné a pomocné premenné	voľní členovia (Riešenie)	Odhadované postoj
Premenné		voľní členovia (Riešenie)	Odhadované postoj

3. krok. Skontrolujeme splnenie kritéria optimality - prítomnosť negatívnych koeficientov v poslednom riadku. Ak také neexistujú, potom je riešenie optimálne a F * = co, základné premenné sa rovnajú zodpovedajúcim koeficientom bj, nebázické premenné sa rovnajú nule, tj. X * = (b 1, b 2, ..., bm , 0,…, 0).

4. krok... Ak nie je splnené kritérium optimality, potom rozlišovací stĺpec s určuje najväčší záporný koeficient v absolútnej hodnote v poslednom (odhadovanom) riadku.

Na určenie rozlišovacej čiary vypočítame odhadované pomery a vyplňte posledný stĺpec tabuľky.

Odhadovaný pomer i-tého radu je

 ak b i a a majú rôzne znaky;

О ak b i = 0 a а je<0;

 ak a je = 0;

0, ak b i = 0 a a je> 0;

V stĺpci hodnotových vzťahov nájdeme minimálny prvok min ktorý definuje permisívny reťazec g.

Ak neexistuje minimum, problém nemá žiadne konečné optimálne I a je neriešiteľný.

Na priesečníku rozlišovacieho riadku a stĺpca je rozlišovací prvok a gs.

5. krok... Zostavíme nasledujúcu tabuľku. Pre to

Prejdeme k tretiemu kroku.

M-metóda Niekedy pri riešení LPP v matici koeficientov s neznámymi sústavami obmedzení neexistujú jednotkové stĺpce, z ktorých by bolo možné zostaviť jednotkovú maticu, t.j. je problém s výberom základných premenných, alebo je pôvodné riešenie neprípustné. V takýchto prípadoch použite metóda umelého základu (M - metóda). Zavádzajú sa všetky obmedzenia, kde neexistujú žiadne základné premenné umelé premenné. V objektívnej funkcii sú zavedené umelé premenné s koeficientom (- M) pre problémy s max a s koeficientom (+ M) pre problémy s min, kde M je dostatočne veľké kladné číslo... Potom je rozšírený problém vyriešený podľa pravidiel simplexovej metódy. Ak sú všetky umelé premenné rovné nule, t.j. sú vylúčené zo základu, potom sa buď dosiahne optimálne riešenie pôvodného problému, alebo sa pôvodný problém ďalej vyrieši a nájde sa jeho optimálne riešenie, alebo sa stanoví jeho nerozhodnuteľnosť. Ak sa ukáže, že aspoň jedna z umelých premenných je nenulová, pôvodný problém nemá riešenie

Univerzálna metóda na riešenie problémov LP sa nazýva simplexová metóda. Aplikácia tejto metódy a jej najbežnejšia modifikácia - dvojfázová simplexová metóda.

V grafickej metóde riešenia problémov LP sme vlastne vybrali z množiny vrcholov patriacich k hranici množiny riešení do sústavy nerovností taký vrchol, v ktorom hodnota objektívnej funkcie dosiahla svoje maximum (minimum). V prípade dvoch premenných je táto metóda úplne vizuálna a umožňuje vám rýchlo nájsť riešenie problému.

Ak sú v probléme tri alebo viac premenných a v skutočných ekonomických problémoch je to presne táto situácia, je ťažké si predstaviť oblasť riešení systému obmedzení. Takéto úlohy sa riešia pomocou simplexová metóda alebo metódou postupného zlepšovania. Myšlienka metódy je jednoduchá a je nasledovná.

Podľa istého pravidla sa nájde pôvodný referenčný plán (nejaký vrchol oblasti obmedzenia). Kontroluje sa, či je plán optimálny. Ak áno, problém je vyriešený. Ak nie, potom choďte na ďalší vylepšený plán - na ďalší vrchol. hodnota objektívnej funkcie v tomto pláne (v tomto vrchole) je očividne lepšia ako v predchádzajúcom. Algoritmus prechodu sa vykonáva pomocou nejakého výpočtového kroku, ktorý je vhodne zapísaný vo forme tabuliek, tzv simplexové tabuľky ... Pretože existuje konečný počet vrcholov, v konečnom počte krokov dospejeme k optimálnemu riešeniu.

Uvažujme o simplexovej metóde pomocou konkrétneho príkladu problému zostavenia plánu.

Znovu si všimnite, že simplexová metóda je použiteľná na riešenie kanonických problémov LP redukovaných na špeciálnu formu, t. J. Majúcich základ, pozitívne pravé strany a objektívnu funkciu vyjadrenú v podobe nezákladných premenných. Ak sa úloha nezredukuje na špeciálny formulár, potom sú potrebné ďalšie kroky, o ktorých budeme hovoriť neskôr.

Uvažujme o probléme výrobného plánu, ktorý predtým postavil model a zredukoval ho na špeciálnu formu.

Úloha.

Na výrobu výrobkov A a V. sklad môže uvoľniť najviac 80 jednotiek surovín. Navyše na výrobu výrobku A spotrebujú sa dve jednotky a výrobky V.- jedna jednotka surovín. Je potrebné naplánovať výrobu tak, aby bol zaistený najväčší zisk, ak ide o výrobky A je potrebné vyrobiť najviac 50 kusov a výrobky V.- nie viac ako 40 ks. Navyše zisk z predaja jedného produktu A- 5 rubľov a od V.- 3 rubľov.

Zostrojme matematický model, označujúci pre NS 1 počet produktov A v pláne, pre NS 2 - počet výrobkov V.... potom bude systém obmedzení vyzerať takto:

x 1 ≤50
x 2 ≤40
2x 1 + x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 + 3x 2 → max

Prenesme problém do kanonickej podoby zavedením ďalších premenných:

x 1 + x 3 = 50
x 2 + x 4 = 40
2x 1 + x 2 + x 5 = 80
x 1 ≥0, x 2 ≥0
5x 1 + 3x 2 → max
-F = -5x 1 -3x 2 → min.

Tento problém má špeciálny tvar (na základe ktorého sú pravé strany nezáporné). Dá sa to vyriešiť pomocou simplexovej metódy.

Jaetapa. Zápis úlohy do simplexovej tabuľky. Medzi systémom obmedzení problému (3.10) a simplexovou tabuľkou existuje individuálna korešpondencia. V tabuľke je toľko riadkov, koľko je v väzbovom systéme rovností, a rovnako veľa stĺpcov ako voľných premenných. Základné premenné vypĺňajú prvý stĺpec, voľné premenné horný riadok tabuľky. Spodný riadok sa nazýva indexový riadok a obsahuje koeficienty premenných v objektívnej funkcii. Ak vo funkcii nie je žiadny voľný výraz, na začiatku je 0 napísané v pravom dolnom rohu; ak existuje, zapíšeme to opačným znamienkom. Na tomto mieste (v pravom dolnom rohu) bude hodnota objektívnej funkcie, ktorá by sa pri prechode z jedného stolu na druhý mala zvyšovať v absolútnej hodnote. Náš systém obmedzení teda zodpovedá tabuľke 3.4 a môžeme pristúpiť k II. Fáze riešenia.

Tabuľka 3.4

základná línia			zadarmo

IIetapa... Kontrola optimality plánu podpory.

Táto tabuľka 3.4 zodpovedá nasledujúcemu základnému plánu:

(NS 1 , NS 2 , NS 3 , NS 4 , NS 5) = (0, 0, 50, 40, 80).

Voľné premenné NS 1 , NS 2 sú 0; NS 1 = 0, NS 2 = 0. A základné premenné NS 3 , NS 4 , NS 5 prevezmite hodnoty NS 3 = 50, NS 4 = 40, NS 5 = 80 - zo stĺpca voľných členov. Hodnota objektívnej funkcie:

-F = - 5NS 1 - 3NS 2 = -5 0 - 3 0 = 0.

Našou úlohou je skontrolovať, či je daný základný plán optimálny. Na to musíte vidieť indexový riadok - riadok objektívnej funkcie F.

Sú možné rôzne situácie.

1. V indexe F-reťazec neobsahuje žiadne negatívne prvky. To znamená, že plán je optimálny, môžete napísať riešenie problému. Objektívna funkcia dosiahla svoju optimálnu hodnotu rovnajúcu sa číslu v pravom dolnom rohu s opačným znamienkom. Prejdeme do fázy IV.

2. Riadok indexu obsahuje najmenej jeden negatívny prvok, ktorého stĺpec neobsahuje žiadne pozitívne prvky. Potom usúdime, že objektívna funkcia F→ ∞ sa neobmedzene znižuje.

3. Riadok indexu obsahuje negatívny prvok, v ktorom je najmenej jeden pozitívny prvok. Potom prejdeme k ďalšej fáze III. prepočítame tabuľku a zdokonalíme základný plán.

IIIetapa... Zlepšenie základnej línie.

Z negatívnych prvkov indexu F-Riadky vyberajú najväčší z modulov, zavolajte zodpovedajúce rozlíšenie stĺpcov a označte „“.

Na výber rozlišovacieho riadku je potrebné vypočítať pomery prvkov stĺpca voľného člena iba Komu pozitívne permisívne stĺpcové prvky. Zo získaných vzťahov vyberte minimum. Zodpovedajúci prvok, pri ktorom sa dosiahne minimum, sa nazýva rozlišovací. Zvýrazníme to štvorcom.

V našom prípade je prvok 2 permisívny. Riadok zodpovedajúci tomuto prvku sa nazýva aj rozlišovací (tabuľka 3.5).

Tabuľka 3.5

Po zvolení rozlišovacieho prvku prepočítame tabuľku podľa pravidiel:

1. V novej tabuľke rovnakej veľkosti ako predtým sa prehodia premenné rozlišujúceho riadka a stĺpca, čo zodpovedá prechodu na nový základ. V našom prípade: NS 1 je zahrnutý v základe, namiesto NS 5, ktorý opúšťa základ a je teraz voľný (tabuľka 3.6).

Tabuľka 3.6

2. Na miesto rozlišovacieho prvku 2 napíšte jeho inverzné číslo ½.

3. Prvky rozlišovacej čiary sú rozdelené rozlišovacím prvkom.

4. Prvky rozlišovacieho stĺpca sú rozdelené rozlišovacím prvkom a zapísané opačným znamienkom.

5. Aby sme vyplnili zvyšné prvky tabuľky 3.6, prepočítame podľa pravidla pre obdĺžnik. Predpokladajme, že chceme počítať prvok na pozícii 50.

Tento prvok mentálne spojíme s rozlišovacím, nájdeme súčin, odčítame súčin prvkov nachádzajúcich sa na druhej uhlopriečke výsledného obdĺžnika. Rozdiel delíme na rozlišovací prvok.

Takže. Na miesto, kde bolo 50. Napíšeme 10. Podobne:
, , , .

Tabuľka 3.7

Máme novú tabuľku 3.7, základnými premennými sú teraz premenné (x 3, x 4, x 1). Hodnota objektívnej funkcie sa rovnala -200, t.j. poklesla. Na kontrolu optimality tohto základného riešenia je potrebné znova prejsť na stupeň II. Proces je evidentne konečný, kritériom zastavenia sú body 1 a 2 etapy II.

Nechajme riešenie problému dotiahnuť do konca. Za týmto účelom skontrolujte riadok indexu a v ňom vidíte záporný prvok –½, zavolajte zodpovedajúce riešenie stĺpcov a podľa etapy III prepočítajte tabuľku. Keď sme zostavili vzťahy a vybrali sme medzi nimi minimum = 40, určili sme rozlišovací prvok 1. Teraz vykonáme prepočet podľa pravidiel 2-5.

Tabuľka 3.8

Po prepočítaní tabuľky sa uistíme, že v riadku indexu nie sú žiadne negatívne prvky, preto je problém vyriešený, základný plán je optimálny.

IVetapa... Vypísanie optimálneho riešenia.

Ak sa simplexová metóda zastavila podľa bodu 1 etapy II, riešenie problému je zapísané nasledovne. Základné premenné preberajú hodnoty stĺpca voľných členov. V našom prípade NS 3 = 30, NS 2 = 40, NS 1 = 20. Voľné premenné sú 0, NS 5 = 0, NS 4 = 0. Cieľová funkcia preberá hodnotu posledného prvku stĺpca voľných členov s opačným znamienkom: - F = -220 → F= 220, v našom prípade bola funkcia skúmaná min a spočiatku F→ max, takže v skutočnosti sa značka dvakrát zmenila. Takže, NS* = (20, 40, 30, 0, 0), F* = 220. Odpoveď na problém:

Je potrebné zahrnúť 20 výrobkov typu A, 40 produktov typu B, pričom zisk bude maximálny a bude sa rovnať 220 rubľom.

Na konci tejto časti uvádzame vývojový diagram algoritmu simplexovej metódy, ktorý presne opakuje kroky, ale pre niektorých čitateľov bude možno jednoduchšie ho použiť, pretože šípky označujú jasný smer akcie.

Odkazy nad rámčekmi vo vývojovom diagrame ukazujú, do ktorej fázy alebo podčasti patrí zodpovedajúca transformačná skupina. pravidlo na nájdenie pôvodného základného plánu bude formulované v článku 3.7.

Príklad. Vyriešte nasledujúci problém LP v kanonickej forme pomocou simplexovej metódy.
f (x) = x 1 + 9x 2 + 5x 3 + 3x 4 + 4x 5 + 14x 6 → min
x 1 + x 4 = 20
x 2 + x 5 = 50
x 3 + x 6 = 30
x 4 + x 5 + x 6 = 60
x i ≥ 0, i = 1, ..., 6
Hovorí sa, že problém LP má kanonickú formu, ak všetky obmedzenia (s výnimkou podmienok nezápornosti premenných) majú formu rovností a všetky voľné výrazy sú nezáporné. Máme teda problém v kanonickej forme.
Myšlienka simplexovej metódy je nasledovná. Najprv musíte nájsť nejaký (počiatočný) vrchol mnohostena uskutočniteľných riešení (počiatočné uskutočniteľné základné riešenie). Potom musíte skontrolovať optimálnosť tohto riešenia. Ak je to optimálne, riešenie sa našlo; ak nie, potom choďte na iný vrchol polytopu a znova skontrolujte optimálnosť. Vzhľadom na konečnosť vrcholov mnohostena (dôsledok konečnosti obmedzení problému LP) v konečnom počte „krokov“ nájdeme požadovaný minimálny alebo maximálny bod. Je potrebné poznamenať, že pri prechode z jedného vrcholu do druhého hodnota objektívnej funkcie klesá (v probléme na minimum) alebo sa zvyšuje (v probléme na maximum).
Myšlienka simplexovej metódy je teda založená na troch vlastnostiach problému LP.
Riešenie. Nájsť počiatočné uskutočniteľné základné riešenie, t.j. na určenie základných premenných musí byť systém (5.6) zmenšený na "diagonálny" tvar. Použitím Gaussovej metódy (metóda postupnej eliminácie neznámych) získame z (5.6):
x 2 + x 1 + x 3 = 40
x 4 + x 1 = 20
x 5 -x 1 -x 3 = 10
x 6 + x 3 = 30
Preto sú základné premenné x 2, x 4, x 5, x 6, priradíme im hodnoty rovnajúce sa voľným členom zodpovedajúcich reťazcov: x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,... Premenné x 1 a x 3 nie sú základné: x 1 = 0, x 3 = 0.
Vytvorme počiatočné prípustné základné riešenie
x 0 = (0,40,0,20,10,30) (5,9)
Skontrolovať optimálnosť nájdeného riešenia x 0 z objektívnej funkcie (pomocou systému (5.8)) je potrebné vylúčiť základné premenné a zostrojiť špeciálnu simplexovú tabuľku.
Po odstránení premenných je možné objektívnu funkciu pohodlne zapísať ako:
f (x) = -7x 1 - 14x 3 +880 (5,10)
Teraz pomocou (5.8) - (5.10) zostavíme počiatočnú simplexovú tabuľku:

Nulový riadok obsahuje koeficienty s opačným znamienkom zodpovedajúcich premenných pre objektívnu funkciu. Kritérium optimality (pre problém hľadania minima): prípustné základné riešenie ( x 0) je optimálne, ak nulový riadok neobsahuje ani jedno prísne kladné číslo (nepočítajúc hodnotu objektívnej funkcie (880)). Toto pravidlo platí pre nasledujúce iterácie (tabuľky). Prvky nulového radu sa budú nazývať stĺpcové odhady.
Počiatočné prípustné základné riešenie (5.9) preto nie je optimálne: 7>0, 14>0 .
Nulový stĺpec obsahuje hodnoty základných premenných. Musia byť nezáporné (pozri rovnicu (5.7)). Od prvého do štvrtého riadku sú zapísané koeficienty premenných zo systému (5.8).
Pretože x 0 nie je optimálne, potom musíte prejsť na iný vrchol mnohostena uskutočniteľných riešení (zostrojte nový b.d.). Na to musíte nájsť pivot a vykonať určitú transformáciu (simplexová transformácia).
Najprv nájdeme vedúci prvok tabuľky, ktorý stojí na priesečníku vedúceho stĺpca (stĺpca s najvyšším kladným skóre) a vedúceho riadka (riadok zodpovedajúci minimálnemu pomeru prvkov nulového stĺpca k zodpovedajúce prvky (prísne kladné) vedúceho stĺpca).
V tabuľke 1 je vedúci stĺpec tretím stĺpcom a vedúci riadok je štvrtým riadkom. (min. (40 / 1,30 / 1) = 30/1) sú označené šípkami a vedúci prvok je označený kruhom. Hostiteľ naznačuje, že základná premenná x 6 je potrebné nahradiť nie základným x 3... Potom budú nové základné premenné x 2, x 3, x 4, x 5,, a non -basic - x 1, x 6,... To znamená prechod na nový vrchol mnohostena uskutočniteľných riešení. Nájsť súradnicové hodnoty nového uskutočniteľného základného riešenia x 00 musíte vytvoriť novú simplexnú tabuľku a vykonať v nej elementárne transformácie:
a) rozdeľte všetky prvky vedúcej čiary na vodiaci prvok, čím sa vodiaci prvok zmení na 1 (pre jednoduchosť výpočtov);
b) pomocou vedúceho prvku (rovná sa 1) premení všetky prvky vedúceho stĺpca na nuly (podobne ako metóda eliminácie neznámych);
V dôsledku toho sa v nulovom stĺpci získajú hodnoty nových základných premenných x 2, x 3, x 4, x 5,(pozri tabuľku 2) - základné súčasti nového vrcholu x 00(nie základné prvky x 1 = 0, x 6 = 0,).

Ako ukazuje tabuľka 2, nové základné riešenie x 00 = (0,10,30,20,40,0) neoptimálne (nulový riadok má nezáporné skóre 7). Preto s pivotným prvkom 1 (pozri tabuľku 2) zostavíme novú simplexovú tabuľku, t.j. vybudovanie nového uskutočniteľného základného riešenia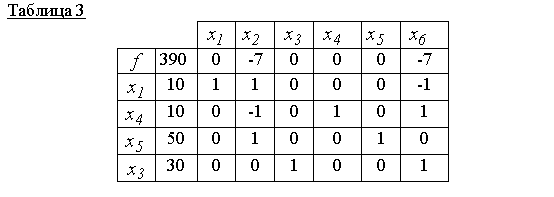

Tabuľka 3 zodpovedá prípustnému základnému riešeniu x 000 = (10,0,30,10,50,0) a je to optimálne, pretože v nulovom riadku nie sú žiadne pozitívne hodnotenia. Preto f (x 000) = 390 je minimálna hodnota objektívnej funkcie.
Odpoveď: x 000 = (10, 0, 30, 10, 50, 0)- minimálny bod, f (x 000) = 390.

Podmienene štandardný problém lineárneho programovania

Nasledujúce úlohy musíte vykonať v uvedenom poradí.

Nájdite optimálny plán pre priamy problém:
a) grafická metóda;
b) simplexová metóda (na zostavenie počiatočného referenčného plánu sa odporúča použiť metódu na umelom základe).
Vytvorte dvojitý problém.
Nájdite optimálny plán duálnej úlohy z grafického riešenia priamky pomocou komplementárnych podmienok vôle.
Nájdite optimálny plán pre duálny problém podľa prvej vety o dualite pomocou konečnej simplexovej tabuľky získanej riešením priameho problému (pozri položku 1b). Skontrolujte tvrdenie „Hodnoty objektívnych funkcií dvojice dvojitých problémov sa zhodujú s ich optimálnym riešením“.
Vyriešte duálny problém simplexovou metódou a potom pomocou konečnej simplexovej tabuľky duálneho problému nájdite optimálny plán priameho problému podľa prvej vety o dualite. Výsledok porovnajte s výsledkom, ktorý bol získaný grafickou metódou (pozri položku 1a).
Nájdite optimálne celočíselné riešenie:
a) grafická metóda;
b) Gomoriho metódou.
Porovnajte hodnoty funkcií celočíselných a neceločíselných riešení

Otázky sebaovládania

Ako sa vytvára simplexová tabuľka?
Ako sa zmena základu premieta do tabuľky?
Formulovať kritérium zastavenia pre simplexovú metódu.
Ako zorganizovať prepočet tabuľky?
S ktorým riadkom je vhodné začať prepočítavať tabuľku?

Ak chcete povoliť spustenie apletu na počítači, postupujte takto - kliknite na položky Štart> Ovládací panel> Programy> Java. V okne Ovládací panel Java vyberte kartu Zabezpečenie, kliknite na tlačidlo Upraviť zoznam stránok, tlačidlo na pridanie a do panela s adresou prehliadača vložte do voľného poľa cestu k tejto stránke. Potom stlačíme tlačidlá OK a potom reštartujeme počítač.

Ak chcete spustiť aplet, kliknite na tlačidlo „Simplex“. Ak nie je tlačidlo „Simplex“ nad týmto riadkom viditeľné, Java v počítači nie je nainštalovaná.

Po kliknutí na tlačidlo „Simplex“ sa zobrazí prvé okno na zadanie počtu premenných a počtu obmedzení úlohy pre simplexovú metódu.

Po kliknutí na tlačidlo „ok“ sa zobrazí okno na zadanie ostatných údajov o úlohe pre simplexovú metódu: režim zobrazenia (desatinné zlomky alebo obyčajné zlomky), typ kritéria úlohy min alebo max, zadanie koeficientov objektívnej funkcie a koeficienty obmedzovacieho systému so znakmi „≤“, „≥“ alebo „=“, obmedzenia tvaru х i ≥ 0 nie je potrebné zadávať, ich zohľadňuje vo svojom algoritme.

Po kliknutí na tlačidlo „Vyriešiť“ sa zobrazí okno s výsledkami riešenia problému .Okno sa skladá z dvoch častí, v hornej časti je textové pole obsahujúce popis redukcie pôvodného problému na kanonický tvar, ktorý slúži na zostavenie prvej simplexovej tabuľky. V spodnej časti okna na table s kartami sú jednostranné tabuľky každej iterácie s malým textovým poľom v spodnej časti, ktoré označuje stĺpec rozlíšenia, riadky rozlíšenia a ďalšie informácie, vďaka ktorým je program výukovým programom. Na karte s optimálnou (poslednou) tabuľkou je v textovom poli zobrazené získané optimálne riešenie problému.

Akékoľvek zistené chyby a komentáre k apletu pošlite na adresu [chránené e -mailom] alebo zavolajte na 8 962 700 77 06, za čo vám budeme veľmi vďační.

Program M-metódy

Program na riešenie dopravného problému

Tu je manuálne (nie apletové) riešenie dvoch problémov pomocou simplexovej metódy (podobné ako riešenie pomocou apletu) s podrobnými vysvetleniami, aby ste porozumeli algoritmu na riešenie problémov. Prvý problém obsahuje znaky nerovnosti iba „≤“ (problém s počiatočným základom), druhý môže obsahovať znaky „≥“, „≤“ alebo „=“ (problém s umelým základom), riešia sa rôznymi spôsobmi .

Jednoduchá metóda, riešenie problému s počiatočným základom

1)Jednoduchá metóda pre problém s počiatočným základom (všetky znaky obmedzení nerovnosti „≤“).

Zapíšeme úlohu do kanonický forma, t.j. obmedzenia nerovnosti je možné prepísať ako rovnosti pridaním súvaha premenné:

Tento systém je systém so základom (základ s 1, s 2, s 3, každý z nich je zahrnutý iba v jednej rovnici systému s koeficientom 1), x 1 a x 2 sú voľné premenné. Problémy, ktoré sa riešia simplexovou metódou, musia mať nasledujúce dve vlastnosti:
- sústava obmedzení musí byť sústavou rovníc na základe;
- voľné termíny všetkých rovníc v systéme musia byť nezáporné.

Výsledný systém je systém na základe a jeho voľné výrazy sú nezáporné; preto je možné použiť simplexovú metódu. Zostavme prvú simplexovú tabuľku (Iterácia 0), t.j. tabuľka koeficientov objektívnej funkcie a sústava rovníc pre zodpovedajúce premenné. Tu „BP“ znamená stĺpec základných premenných, „Riešenie“ - stĺpec pravých strán rovníc systému. Riešenie nie je optimálne, pretože v riadku z sú negatívne koeficienty.

iterácia 0

BP	Riešenie	Postoj

Aby sme vylepšili riešenie, prejdeme k ďalšej iterácii a získame nasledujúcu simplexnú tabuľku. Ak to chcete urobiť, musíte si vybrať permisívny stĺpček, t.j. premenná, ktorá bude zahrnutá do základu pri ďalšej iterácii. Je vybraný najväčším záporným koeficientom v absolútnej hodnote v riadku z (v maximálnom probléme) -v počiatočnej iterácii je to stĺpec x 2 (koeficient -6).

Potom sa vyberie permisívna struna, t.j. premenná, ktorá opustí základ pri ďalšej iterácii. Je vybraný najmenším pomerom stĺpca „Rozhodnutie“ k zodpovedajúcim pozitívnym prvkom rozlišovacieho stĺpca (stĺpček „Pomer“) - v počiatočnej iterácii je to riadok s 3 (koeficient 20).

Povolený prvok je na priesečníku rozlišovacieho stĺpca a rozlišovacieho riadku, jeho bunka je zvýraznená, rovná sa 1. Preto pri ďalšej iterácii premenná x 2 nahradí s 3 v základe. Všimnite si toho, že vzťah nie je hľadaný v riadku z, ale je tam vložená pomlčka „-“. Ak existujú rovnaké minimálne vzťahy, vyberie sa ktorýkoľvek z nich. Ak sú v stĺpci rozlíšenia všetky koeficienty menšie alebo rovné 0, potom je riešenie problému nekonečné.

2) Výpočet z-riadka tabuľky „Iterácia 1“. Namiesto -6 v prvom riadku (riadok z) v stĺpci x 2 tabuľky Iterácie 0 by malo byť 0 v prvom riadku tabuľky Iterácie 1. Za týmto účelom vynásobíme všetky prvky riadku x 2 tabuľky „Iterácia 1“ 0 1 0 0 1 20 číslom 6, dostaneme 0 6 0 0 6 120 a tento riadok pripočítame k prvému riadku (z - riadok) tabuľka "Iterácia 0" -4 -6 0 0 0 0, dostaneme -4 0 0 0 6 120. V stĺpci x 2 sa objaví nula 0, cieľ je dosiahnutý. Povolené prvky stĺpca x 2 sú zvýraznené červenou farbou.

4) Výpočet riadku s 2 tabuľky „Iterácia 1“. Na mieste 3 v s 2 riadku tabuľky „Iterácia 0“ musí byť v tabuľke „Iterácia 1“ 0. Za týmto účelom vynásobíme všetky prvky riadku x 2 tabuľky „Iterácia 1“ 0 1 0 0 1 20 číslom -3, dostaneme 0 -3 0 0 -3 -60 a tento riadok pridáme s s 2 - riadok tabuľky „Iterácia 0“ 1 3 0 1 0 72, dostaneme riadok 1 0 0 1 -3 12. V stĺpci x 2 sa získa požadovaná 0. Stĺpec x 2 v tabuľke „Iterácia 1“ má staň sa jedným, obsahuje jeden 1 a zvyšok 0.

Riadky tabuľky „Iterácia 1“ sa získajú podľa nasledujúceho pravidla:

Nový riadok = starý riadok - (faktor stĺpca rozlíšenia starého riadka) * (nový riadok rozlíšenia).

Napríklad pre reťazec z máme:

Starý reťazec z (-4 -6 0 0 0 0)
- ( - 6) * Nový reťazec rozlíšenia - (0-6 0 0 -6 -120)
= Nový z-riadok(-4 0 0 0 6 120) .

Pri nasledujúcich tabuľkách sa prepočítavanie prvkov tabuľky robí rovnako, preto to vynechávame.

iterácia 1

						Riešenie	Postoj

Iterácia 2

						Riešenie	Postoj

Rozlišovací stĺpec s 3, rozlišovací riadok s 1, s 1 opúšťa základ, s 3 vstupuje do základu.

Iterácia 3

						Riešenie	Postoj

V rade z sú všetky koeficienty nezáporné, preto je optimálne riešenie x 1 = 24, x 2 = 16, z max = 192.

Jednoduchá metóda, riešenie problému na umelom základe

2) Vyriešme problém na umelom základe (aspoň jeden znak obmedzenia nerovnosti „≥“ alebo „=“).

Napíšme problém v kanonickej forme (vo forme sústavy rovníc, ktorá vyžaduje simplexovú metódu), na to zavedieme dve premenné x 3 ≥ 0 a x 4 ≥ 0 získame:

Sústava obmedzení ponúka iba jednu prípustnú základnú premennú x 4, iba je zahrnutá iba v jednej rovnici v tretej s koeficientom 1, takže k prvej a druhej rovnici pridáme umelé premenné R 1 ≥ 0 a R 2 ≥ 0 .obmedzenia rovníc musia byť systémom so základom, t.j. v každej rovnici musí byť premenná s koeficientom 1, ktorá je zahrnutá iba v jednej rovnici systému, v našom prípade je to R 1, R 2 a x 4. Dostali sme takzvaný M-problém:

Tento systém je systém, na základe ktorého R 1, R 2 a x 4 sú základné premenné a x 1, x 2 a x 3 sú voľné premenné, voľné termíny všetkých rovníc nie sú záporné. Na vyriešenie problému preto možno použiť simplexovú metódu. Zapíšeme si počiatočnú simplexovú tabuľku:

iterácia 0

	Riešenie	Postoj
-16

Do tabuľky bol pridaný riadok „Hodnotenie“ pre úlohy s umelým základom. Získame ho súčtom zodpovedajúcich koeficientov riadkov s umelými premennými (R) s opačným znamienkom. V tabuľke bude prítomný, pokiaľ je v základe aspoň jedna z umelých premenných. Podľa najväčšieho modulo negatívneho koeficientu v riadku „Skóre“ je rozlišovací stĺpec určený, keď je v tabuľke. Keď riadok „Skóre“ opustí tabuľku (v základe nie sú žiadne umelé premenné), rozlišovací stĺpec bude určený riadkom z, ako pri probléme s počiatočným základom. V tejto tabuľke je rozlišovací stĺpec x 2, je vybraný podľa najväčšieho modulo negatívneho odhadu (-7). Rozlišovací riadok R2 sa vyberie podľa najmenšieho pomeru stĺpca „Rozhodnutie“ k zodpovedajúcim pozitívnym prvkom rozlišovacieho stĺpca, ako v prípade problému bez umelých premenných. To znamená, že pri ďalšej iterácii prejde premenná x 2 z voľnej na základnú a premenná R 2 zo základnej na voľnú. Napíšme nasledujúcu simplexnú tabuľku:

Prípustný stĺpec x 1, permisívny riadok R 1, R 1 opúšťa základ, x 1 vstupuje do základu. Potom v základe nezostanú žiadne umelé premenné, takže v nasledujúcej tabuľke nie je riadok „Vyhodnotenie“:

iterácia 2

							Riešenie	Postoj

Ďalej je v stĺpci z vybratý rozlišovací stĺpec. V riadku z sú všetky koeficienty nezáporné, okrem koeficientu figuríny R 1, ktorý neovplyvňuje optimálnosť, keď je figurína mimo základ. Preto sa získa optimálne riešenie x 1 = 6/5; x 2 = 3/5; z max = 72/5.

Špeciálne prípady jednoduchej metódy

1) Keď je priamka (ak sa uvažuje s problémom dvojrozmerného lineárneho programovania a vo všeobecnom prípade s hyperplane) predstavujúcou objektívnu funkciu, je rovnobežná s priamkou (hyperplane) zodpovedajúcou jednému z obmedzení nerovnosti (ktorá je splnená v optimálnom bode ako presná rovnosť), objektívna funkcia potrebuje jeden a je tiež optimálnou hodnotou pre niektorú množinu bodov hranice regiónu realizovateľných riešení. Tieto riešenia sa nazývajú alternatívne optimálne riešenia... Dostupnosť alternatívnych riešení môže určiť optimálna simplexová tabuľka. Ak riadok z optimálnej tabuľky obsahuje nulové koeficienty nebázických premenných, existujú alternatívne riešenia.

2) Ak sú v rozlišovacom stĺpci simplexovej tabuľky všetky koeficienty menšie alebo rovné nule, potom nemožno vybrať rozlišovací riadok, v tomto prípade je riešenie bez obmedzenia.

3) Ak sú obmedzenia problému s lineárnym programovaním nekonzistentné (t. J. Nie je ich možné vykonať súčasne), problém nemá žiadne uskutočniteľné riešenia. Táto situácia nemôže nastať, ak všetky nerovnosti, ktoré tvoria systém obmedzení, sú typu „≤“ s nezápornými pravostrannými stranami, pretože v tomto prípade môžu ďalšie premenné predstavovať uskutočniteľné riešenie. Pre ostatné typy obmedzení sa používajú umelé premenné. Ak má problém riešenie, potom v optimálnej tabuľke v základe neexistujú žiadne umelé premenné (R i). Ak tam sú, problém nemá žiadne riešenia.