Arányos szakaszok derékszögű háromszögben. Lecke "arányos szakaszok derékszögű háromszögben" Hogyan keressünk arányos szakaszokat egy derékszögű háromszögben
40. lecke C. b. a. h. C. ie. H. ac. A. V. A derékszög csúcsából húzott derékszögű háromszög magassága a háromszöget 2 hasonló derékszögű háromszögre osztja, amelyek mindegyike hasonló egy adott háromszöghöz. Derékszögű háromszögek hasonlóságának jele. Két derékszögű háromszög hasonló, ha mindegyiknek azonos a hegyesszöge. Az XY szakaszt az AB és CD szakaszok átlagos arányosságának (geometriai átlagának) nevezzük, ha Tulajdonság 1. A derékszög csúcsából húzott derékszögű háromszög magassága a szárak hipotenuzusra vetületei közötti arányos átlag. 2. tulajdonság. A derékszögű háromszög szára a befogó és ennek a lábnak a befogóra való vetülete közötti arányos átlag.
28. dia az előadásból "Geometria "Hasonló háromszögek"". Az archívum mérete a prezentációval együtt 232 KB.Geometria 8. évfolyam
egyéb előadások összefoglalója"Problémák megoldása a Pitagorasz-tételre" - ABC egyenlő szárú háromszög. A Pitagorasz-tétel gyakorlati alkalmazása. Az ABCD egy négyszög. Négyzet alakú terület. Találd meg a napot. Bizonyíték. Egyenlőszárú trapéz alapjai. Tekintsük a Pitagorasz-tételt. Egy négyszög területe. Téglalap alakú háromszögek. Pitagorasz tétel. A hipotenusz négyzete egyenlő a lábak négyzeteinek összegével.
"A paralelogramma területének megtalálása" - Alapítvány. Magasság. A paralelogramma magasságának meghatározása. Derékszögű háromszögek egyenlőségének jelei. A paralelogramma területe. Keresse meg a háromszög területét. Terület tulajdonságai. szóbeli gyakorlatok. Keresse meg a paralelogramma területét. Párhuzamos magasságok. Keresse meg a négyzet kerületét. Egy háromszög területe. Keresse meg a négyzet területét. Keresse meg a téglalap területét. Négyzet alakú terület.
„Kvadrat 8. osztály” - Fekete négyzet. A szóbeli munka feladatai a tér kerületében. Négyzet alakú terület. Négyzet alakú jelek. A tér közöttünk van. A négyzet olyan téglalap, amelynek minden oldala egyenlő. Négyzet. Táska négyzet alakú alappal. szóbeli feladatok. Hány négyzet látható a képen. Négyzet alakú ingatlanok. Gazdag kereskedő. Feladatok szóbeli munkához a tér területén. A négyzet kerülete.
"Axiális szimmetria meghatározása" - ugyanazon a merőlegesen fekvő pontok. Rajzolj két vonalat. Építkezés. Pontok ábrázolása. Nyom. Axiális szimmetriával nem rendelkező ábrák. Szakasz. Hiányzó koordináták. Ábra. Olyan alakzatok, amelyeknek kettőnél több szimmetriatengelye van. Szimmetria. Szimmetria a költészetben. Építs háromszögeket. Szimmetriatengelyek. Szegmens felépítése. Pont építése. Két szimmetriatengelyű ábrák. Népek. Háromszögek. Arányosság.
"Hasonló háromszögek meghatározása" - Sokszögek. arányos vágások. A hasonló háromszögek területének aránya. Két háromszöget hasonlónak nevezünk. Körülmények. Szerkesszünk háromszöget, amelynek két szöge és a csúcsponton lévő felező. Tegyük fel, hogy meg kell határoznunk a pólus távolságát. A háromszögek hasonlóságának harmadik jele. Építsünk háromszöget. ABC. Az ABC és az ABC háromszögnek három egyenlő oldala van. Egy tárgy magasságának meghatározása.
"A Pitagorasz-tétel megoldása" - Ablakok részei. A legegyszerűbb bizonyíték. Hammurapi. Átlós. Teljes bizonyíték. Bizonyítás kivonással. pythagoreusok. Bizonyítás dekompozíciós módszerrel. A tétel története. Átmérő. Bizonyítás komplementer módszerrel. Epstein bizonyítéka. Kántor. Háromszögek. követői. A Pitagorasz-tétel alkalmazásai. Pitagorasz tétel. A tétel kijelentése. Perigal bizonyítéka. A tétel alkalmazása.
Derékszögű háromszögek hasonlóságának jele
Először mutassuk be a derékszögű háromszögek hasonlóságának jelét.
1. tétel
Derékszögű háromszögek hasonlóságának jele: két derékszögű háromszög hasonló, ha egy-egy hegyesszögük egyenlő (1. ábra).
1. ábra Hasonló derékszögű háromszögek
Bizonyíték.
Adjuk meg, hogy $\angle B=\angle B_1$. Mivel a háromszögek derékszögűek, $\angle A=\angle A_1=(90)^0$. Ezért hasonlóak a háromszögek hasonlóságának első jele szerint.
A tétel bizonyítást nyert.
Magasságtétel derékszögű háromszögben
2. tétel
A derékszög csúcsából húzott derékszögű háromszög magassága a háromszöget két hasonló derékszögű háromszögre osztja, amelyek mindegyike hasonló az adott háromszöghöz.
Bizonyíték.
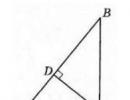
Adjunk egy $ABC$ derékszögű háromszöget $C$ derékszögű. Rajzolja le a $CD$ magasságot (2. ábra).

2. ábra A 2. tétel szemléltetése
Bizonyítsuk be, hogy a $ACD$ és a $BCD$ háromszögek hasonlóak az $ABC$ háromszöghez, és hogy a $ACD$ és $BCD$ háromszögek hasonlóak.
Mivel $\angle ADC=(90)^0$, a $ACD$ háromszög derékszögű. Az $ACD$ és $ABC$ háromszögek $A$ szöge közös, ezért az 1. Tétel szerint a $ACD$ és $ABC$ háromszögek hasonlóak.
Mivel a $\angle BDC=(90)^0$, a $BCD$ háromszög derékszögű. A $BCD$ és $ABC$ háromszögeknek közös a $B$ szöge, ezért az 1. Tétel szerint a $BCD$ és $ABC$ háromszögek hasonlóak.
Tekintsük most a $ACD$ és a $BCD$ háromszögeket
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]
Ezért az 1. Tétel szerint az $ACD$ és a $BCD$ háromszögek hasonlóak.
A tétel bizonyítást nyert.
Átlag arányos
3. tétel
A derékszög csúcsából húzott derékszögű háromszög magassága azoknak a szakaszoknak az átlaga, amelyekre a magasság felosztja ennek a háromszögnek a befogóját.
Bizonyíték.
A 2. Tétel alapján azt kaptuk, hogy az $ACD$ és a $BCD$ háromszögek hasonlóak
A tétel bizonyítást nyert.
4. tétel
A derékszögű háromszög szára a befogó és a befogó szár közé eső szakasza és a szög csúcsából húzott magasság közötti arányos átlag.
Bizonyíték.
A tétel bizonyítása során a 2. ábra jelölését használjuk.
A 2. Tétel szerint az $ACD$ és $ABC$ háromszögek hasonlóak, ezért
A tétel bizonyítást nyert.
Derékszögű háromszögek hasonlóságának jele
Először mutassuk be a derékszögű háromszögek hasonlóságának jelét.
1. tétel
Derékszögű háromszögek hasonlóságának jele: két derékszögű háromszög hasonló, ha egy-egy hegyesszögük egyenlő (1. ábra).
1. ábra Hasonló derékszögű háromszögek
Bizonyíték.
Adjuk meg, hogy $\angle B=\angle B_1$. Mivel a háromszögek derékszögűek, $\angle A=\angle A_1=(90)^0$. Ezért hasonlóak a háromszögek hasonlóságának első jele szerint.
A tétel bizonyítást nyert.
Magasságtétel derékszögű háromszögben
2. tétel
A derékszög csúcsából húzott derékszögű háromszög magassága a háromszöget két hasonló derékszögű háromszögre osztja, amelyek mindegyike hasonló az adott háromszöghöz.
Bizonyíték.
Adjunk egy $ABC$ derékszögű háromszöget $C$ derékszögű. Rajzolja le a $CD$ magasságot (2. ábra).

2. ábra A 2. tétel szemléltetése
Bizonyítsuk be, hogy a $ACD$ és a $BCD$ háromszögek hasonlóak az $ABC$ háromszöghez, és hogy a $ACD$ és $BCD$ háromszögek hasonlóak.
Mivel $\angle ADC=(90)^0$, a $ACD$ háromszög derékszögű. Az $ACD$ és $ABC$ háromszögek $A$ szöge közös, ezért az 1. Tétel szerint a $ACD$ és $ABC$ háromszögek hasonlóak.
Mivel a $\angle BDC=(90)^0$, a $BCD$ háromszög derékszögű. A $BCD$ és $ABC$ háromszögeknek közös a $B$ szöge, ezért az 1. Tétel szerint a $BCD$ és $ABC$ háromszögek hasonlóak.
Tekintsük most a $ACD$ és a $BCD$ háromszögeket
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]
Ezért az 1. Tétel szerint az $ACD$ és a $BCD$ háromszögek hasonlóak.
A tétel bizonyítást nyert.
Átlag arányos
3. tétel
A derékszög csúcsából húzott derékszögű háromszög magassága azoknak a szakaszoknak az átlaga, amelyekre a magasság felosztja ennek a háromszögnek a befogóját.
Bizonyíték.
A 2. Tétel alapján azt kaptuk, hogy az $ACD$ és a $BCD$ háromszögek hasonlóak
A tétel bizonyítást nyert.
4. tétel
A derékszögű háromszög szára a befogó és a befogó szár közé eső szakasza és a szög csúcsából húzott magasság közötti arányos átlag.
Bizonyíték.
A tétel bizonyítása során a 2. ábra jelölését használjuk.
A 2. Tétel szerint az $ACD$ és $ABC$ háromszögek hasonlóak, ezért
A tétel bizonyítást nyert.
Az óra céljai:
- bevezetni a két szakasz átlagos arányos (geometriai középértéke) fogalmát;
- tekintsük a derékszögű háromszög arányos szakaszainak problémáját: a derékszög csúcsából húzott derékszögű háromszög magasságának tulajdonsága;
- a tanulók képességeinek kialakítása a tanult téma felhasználásában a problémamegoldás során.
Az óra típusa: lecke új anyag tanulása.
Terv:
- Szervezési pillanat.
- Tudásfrissítés.
- A derékszög csúcsából húzott derékszögű háromszög magasságának tulajdonságának vizsgálata:
- előkészítő szakasz;
– bevezetés;
- asszimiláció. - A két szegmenssel arányos átlag fogalmának bevezetése.
- A két szegmens átlagarányos fogalmának asszimilációja.
- A következmények igazolása:
- a derékszög csúcsából húzott derékszögű háromszög magassága azoknak a szakaszoknak az átlaga, amelyekre a befogó fel van osztva ezzel a magassággal;
- a derékszögű háromszög szára a befogó és a láb és a magasság közé zárt szegmens közötti arányos átlag. - Problémamegoldás.
- Összegzés.
- Házi feladat beállítása.
Az órák alatt
I. SZERVEZÉS
Sziasztok srácok, foglaljon helyet. Mindenki készen áll a leckére?
Elkezdjük a munkát.
II. AZ ISMERETEK FRISSÍTÉSE
Milyen fontos matematikai fogalmat tanultál meg az előző leckéken? ( a háromszög hasonlóság fogalmával)
- Emlékezzünk, melyik két háromszöget nevezik hasonlónak? (két háromszöget hasonlónak nevezünk, ha a szögeik egyenlőek és az egyik háromszög oldalai arányosak a másik háromszög hasonló oldalaival)
Mivel igazoljuk két háromszög hasonlóságát? (
- Sorolja fel ezeket a jeleket. (fogalmazd meg a háromszögek hasonlóságának három jelét)
III. A DERÉKSZÖG CSÚCSÁBÓL KIVEZETT TÉGSZÖGŰ HÁROMSZÖG MAGASSÁGÁNAK TULAJDONSÁGÁNAK TANULMÁNYOZÁSA
a) előkészítő szakasz
- Srácok, kérlek nézd meg az első diát. ( Függelék) Itt van két derékszögű háromszög - és . és a magasságok, ill. ![]() .
.
1. feladat a) Határozza meg, hogy és hasonlóak-e.
Mivel igazoljuk a háromszögek hasonlóságát? ( a háromszögek hasonlóságának jelei)
(az első jel, mivel a feladatban szereplő háromszögek oldalairól semmit sem tudunk)
. (Két pár: 1. ∟B= ∟B1 (egyenesek), 2. ∟A= ∟A 1)
- Vegyünk egy következtetést. a háromszögek hasonlóságának első jelével ~)
1. b) feladat Határozza meg, hogy és hasonlóak-e.
Milyen hasonlósági kritériumot alkalmazunk és miért? (az első jel, mert a feladatban semmit sem tudunk a háromszögek oldalairól)
Hány egyenlő szögpárt kell megtalálnunk? Találd meg ezeket a párokat (mivel a háromszögek derékszögűek, elég egy pár egyenlő szög: ∟A= ∟A 1)
- Vegyünk egy következtetést. (a háromszögek hasonlóságának első jelével arra a következtetésre jutunk, hogy ezek a háromszögek hasonlóak).
A beszélgetés eredményeként az 1. dia így néz ki:

b) a tétel felfedezése
2. feladat.
Határozza meg, hogy és , és hasonlóak-e. A beszélgetés eredményeként válaszok épülnek fel, melyek tükröződnek a dián.

- Az ábra azt jelezte . Használtuk ezt a mértéket a feladatok kérdéseinek megválaszolásakor? ( Nem, nem használt)
- Srácok, vonja le a következtetést: melyik háromszögekre osztja a derékszög csúcsából húzott magasság a derékszögű háromszöget? (vonja le a következtetést)

- Felmerül a kérdés: vajon ez a két derékszögű háromszög, amelyre a magasság a derékszögű háromszöget osztja, hasonló lesz-e egymáshoz? Próbáljunk egyenlő szögű párokat keresni.
A beszélgetés eredményeként rekord készül:

- És most vonjuk le a teljes következtetést. ( KÖVETKEZTETÉS: a derékszög csúcsából húzott derékszögű háromszög magassága két részre osztja a háromszöget hasonló
- Azt. megfogalmaztunk és bebizonyítottuk a derékszögű háromszög magasságának tulajdonságára vonatkozó tételt.
Állítsuk fel a tétel szerkezetét és készítsünk rajzot. Mit adunk meg a tételben és mit kell bizonyítani? A tanulók a füzetükbe írják:

Bizonyítsuk be a tétel első pontját az új rajzhoz. Milyen hasonlósági kritériumot alkalmazunk és miért? (Először is, mivel a tételben a háromszögek oldalairól semmit sem tudunk)
Hány egyenlő szögpárt kell megtalálnunk? Találd meg ezeket a párokat. (Ebben az esetben elég egy pár: ∟A-általános)
- Vegyünk egy következtetést. A háromszögek hasonlóak. Ennek eredményeként egy példát mutatunk be a tétel megfogalmazására

- Írja meg otthon a második és harmadik pontot maga.
c) a tétel asszimilációja
- Szóval, fogalmazd meg újra a tételt (A derékszög csúcsából húzott derékszögű háromszög magassága két részre osztja a háromszöget hasonló derékszögű háromszögek, amelyek mindegyike hasonló ehhez)
- Hány pár hasonló háromszög található meg ezzel a tétellel "egy derékszögű háromszögben a derékszög csúcsától mért magasság" konstrukcióban? ( Három pár)
A tanulók a következő feladatot kapják:

IV. A KÉT VONAL ÁTLAGOS ARÁNYOSSÁGÁNAK FOGALMÁNAK BEVEZETÉSE
Most egy új koncepciót tanulunk meg.
Figyelem!
Meghatározás. Szakasz XY hívott átlagos arányos (geometriai átlag) szegmensek között ABés CD, ha
(írd füzetbe).
V. A KÉT SOR ÁTLAGOS ARÁNYOSSÁGA FOGALMA TÁRSULÁSA
Most menjünk tovább a következő diára.
1. Feladat. Határozza meg az átlagos arányos MN és KP szakaszok hosszát, ha MN = 9 cm, KP = 16 cm!
- Mit adnak a feladatban? ( Két szegmens és hosszuk: MN = 9 cm, KP = 16 cm)
- Mit kell találnod? ( E szegmensek arányos átlagának hossza)
- Mi az arányos átlag képlete, és hogyan találjuk meg?
(Az adatokat behelyettesítjük a képletbe, és megkeressük az átlagos prop hosszát.)
2. számú feladat. Határozzuk meg az AB szakasz hosszát, ha az AB és CD szakaszok átlagos aránya 90 cm és CD = 100 cm
- Mit adnak a feladatban? (a CD szakasz hossza = 100 cm, és az AB és CD szakaszok átlagos aránya 90 cm)
Mit kell keresni a problémában? ( AB szakasz hossza)
- Hogyan fogjuk megoldani a problémát? (Írjuk fel az átlagos AB és CD arányos szakaszok képletét, fejezzük ki belőle AB hosszát és helyettesítsük be a feladat adatait!)
VI. KÖVETKEZTETÉS
- Jó volt fiúk. És most térjünk vissza a háromszögek hasonlóságához, amelyet a tételben bizonyítottunk. Fogalmazd meg újra a tételt! ( A derékszög csúcsából húzott derékszögű háromszög magassága kettéosztja a háromszöget hasonló derékszögű háromszögek, amelyek mindegyike hasonló egy adotthoz)
- Először használjuk a háromszögek és a hasonlóságot. Mi következik ebből? ( A hasonlóság meghatározása szerint az oldalak arányosak a hasonló oldalakkal)
- Milyen egyenlőség érhető el az arányosság alaptulajdonsága használatával? ()
– Expressz CD-t és vonjon le következtetést (![]() ;
;![]() .
.
Következtetés: a derékszög csúcsából húzott derékszögű háromszög magassága azoknak a szakaszoknak az átlaga, amelyekre a befogó el van osztva ezzel a magassággal)
- És most bizonyítsd be magadnak, hogy egy derékszögű háromszög szára átlagosan arányos a befogó és a láb és a magasság közé zárt szegmens között. Megtaláljuk - ...-ból azokat a szegmenseket, amelyekre a befogó fel van osztva ezt a magasságot )
Egy derékszögű háromszög szára a ... (- ... az e láb és a magasság közé zárt hypotenus és a hypotenus szegmense )
– Hol alkalmazzuk a tanult állításokat? ( A problémák megoldása során)
IX. HÁZI FELADAT BEÁLLÍTÁSA
d/z: 571. sz., 572. sz. (a, e), önálló munka füzetben, elmélet.
Ma egy újabb előadásra hívják fel a figyelmet egy csodálatos és titokzatos témáról - a geometriáról. Ebben az előadásban bemutatjuk a geometriai formák új tulajdonságát, különös tekintettel a derékszögű háromszögek arányos szakaszainak fogalmára.
Először is emlékeznie kell arra, hogy mi a háromszög? Ez a legegyszerűbb sokszög, amely három csúcsból áll, amelyeket három szegmens köt össze. A derékszögű háromszög olyan háromszög, amelyben az egyik szög 90 fokos. Ezekkel már részletesebben is megismerkedhetett korábbi, figyelmébe ajánlott képzési anyagainkban.
Visszatérve tehát mai témánkhoz, sorrendben jelöljük, hogy a 90 fokos szögből megrajzolt derékszögű háromszög magassága két háromszögre osztja, amelyek mind egymáshoz, mind az eredetihez hasonlóak. Az összes érdeklõdõ rajz és grafikon megtalálható a javasolt prezentációban, és javasoljuk, hogy hivatkozzon rájuk, a leírt magyarázat kíséretében.
A fenti tézis grafikus példája a második dián látható. A háromszögek hasonlóak, mert két azonos szögük van. Ha részletesebben adjuk meg, akkor a hipotenuszra süllyesztett magasság derékszöget zár be vele, vagyis már vannak azonos szögek, és mindegyik kialakított szögnek van egy közös szöge is, mint az eredeti. Az eredmény két egymással egyenlő szög. Vagyis a háromszögek hasonlóak.

Jelöljük azt is, hogy mit jelent önmagában az „arányos átlag” vagy „geometriai átlag” fogalma? Ez egy bizonyos XY szegmens az AB és CD szegmensek számára, ha egyenlő a hosszuk szorzatának négyzetgyökével.
Amiből az is következik, hogy egy derékszögű háromszög szára a befogó és ennek a lábnak a befogóra, vagyis a másik lábra való vetülete közötti geometriai átlag.

A derékszögű háromszög másik tulajdonsága, hogy magassága 90 o-os szögből húzva átlagosan arányos a lábak hipotenuszra vetületei között. Ha hivatkozik a prezentációra és a tudomására jutott egyéb anyagokra, látni fogja, hogy ennek a tézisnek a bizonyítéka nagyon egyszerű és hozzáférhető formában. Korábban már bebizonyítottuk, hogy a kapott háromszögek hasonlóak egymáshoz és az eredeti háromszöghez. Ezután ezeknek a geometriai alakzatoknak a lábainak arányát felhasználva arra a következtetésre jutunk, hogy egy derékszögű háromszög magassága egyenesen arányos azon szakaszok szorzatának négyzetgyökével, amelyek a magasságból való lecsökkentés eredményeként jöttek létre. az eredeti háromszög derékszöge.

Az előadásban az utolsó dolog, hogy egy derékszögű háromszög szára a szár és a 90 fokkal egyenlő szögből húzott magasság között elhelyezkedő befogó és szakaszának geometriai átlaga. Ezt az esetet oldalról kell szemlélni, hogy ezek a háromszögek hasonlóak egymáshoz, és az egyik lábát a másik befogója kapja. De ezt részletesebben megismerheti a javasolt anyagok tanulmányozásával.