Algorithme de la méthode simplex. Méthode simplex pour résoudre zlp. Problème de programmation linéaire conditionnellement standard

Si vous devez résoudre un problème de programmation linéaire à l'aide de tables simplex, notre service en ligne vous sera d'une grande aide. La méthode du simplexe implique une énumération séquentielle de tous les sommets de la plage de valeurs admissibles afin de trouver le sommet où la fonction prend une valeur extrême. À la première étape, une solution est trouvée, qui est améliorée à chaque étape suivante. Cette solution est dite basique. Voici une séquence d'actions lors de la résolution d'un problème de programmation linéaire à l'aide de la méthode du simplexe :

Premier pas. Dans le tableau compilé, vous devez tout d'abord regarder la colonne avec les membres gratuits. S'il contient des éléments négatifs, il est alors nécessaire de passer à la deuxième étape, sinon à la cinquième.

Deuxième étape. A la deuxième étape, il est nécessaire de décider quelle variable exclure de la base, et laquelle inclure, afin de recalculer la table simplex. Pour ce faire, parcourez la colonne des membres libres et trouvez-y un élément négatif. La ligne avec un élément négatif sera appelée la ligne principale. On y trouve l'élément négatif maximum en valeur absolue, la colonne correspondante - le suiveur. S'il y a des valeurs négatives parmi les membres libres, mais pas dans la ligne correspondante, un tel tableau n'aura pas de solutions. En changeant dans la première ligne, celui de la colonne des membres libres est exclu de la base, et la variable correspondant à la première colonne est incluse dans la base.

Tableau 1.

variables de base	Membres libres sous contraintes	Variables de non-base
variables de base	Membres libres sous contraintes	x 1	x 2	...	x l	...	xn
xn+1	b 1	un 11	un 12	...	un 1l	...	un 1n
xn+2	b 2	un 21	un 22	...	un 2l	...	un 2n
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
xn + r	b2	un r1	un r2	...	un rl	...	un rn
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
xn + m	b m	un m1	un m2	...	un ml	...	un mn
F(x) max	F 0	-c 1	-c 2	...	-c 1	...	-c n

Troisième étape. À la troisième étape, nous recalculons l'ensemble du tableau simplex à l'aide de formules spéciales, ces formules peuvent être vues à l'aide.

Quatrième étape. Si, après recalcul, des éléments négatifs restent dans la colonne des membres libres, passez à la première étape, s'il n'y en a pas, passez à la cinquième.

Cinquième étape. Si vous avez atteint la cinquième étape, alors vous avez trouvé une solution acceptable. Cependant, cela ne signifie pas qu'il est optimal. Il ne sera optimal que si tous les éléments de la ligne F sont positifs. Si ce n'est pas le cas, il est alors nécessaire d'améliorer la solution, pour laquelle nous trouvons la ligne et la colonne de tête pour le prochain recalcul selon l'algorithme suivant. Initialement, nous trouvons le nombre négatif minimum à la ligne F, à l'exclusion de la valeur de la fonction. La colonne avec ce numéro sera la première. Afin de trouver la première ligne, nous trouvons le rapport du membre libre correspondant et de l'élément de la première colonne, à condition qu'ils soient positifs. La relation minimale vous permettra de définir la première ligne. Nous recalculons à nouveau le tableau en utilisant les formules, c'est-à-dire passez à l'étape 3.

Voici une solution manuelle (pas une applet) de deux problèmes par la méthode simplex (similaire à la solution par une applet) avec des explications détaillées afin de comprendre l'algorithme de résolution de problèmes par la méthode simplex. Le premier problème ne contient que des signes d'inégalité "≤" (un problème avec une base initiale), le second peut contenir des signes "≥", "≤" ou "=" (un problème avec une base artificielle), ils sont résolus de différentes manières .

Méthode simplex, résolution d'un problème avec une base initiale

1)Méthode simplex pour un problème avec une base initiale (tous les signes d'inégalité-contraintes "≤").

Écrivons la tâche dans canonique forme, c'est-à-dire les contraintes d'inégalité peuvent être réécrites comme des égalités en ajoutant bilan variables :

Ce système est un système à base (base s 1, s 2, s 3, chacun d'eux est inclus dans une seule équation du système de coefficient 1), x 1 et x 2 sont des variables libres. Les problèmes, dans la solution desquels la méthode du simplexe est utilisée, doivent avoir les deux propriétés suivantes : - le système de contraintes doit être un système d'équations avec une base ; - les termes libres de toutes les équations du système doivent être non négatifs.

Le système résultant est un système avec une base et ses termes libres sont non négatifs ; par conséquent, nous pouvons appliquer méthode du simplexe... Composons la première table du simplexe (Itération 0) pour résoudre le problème sur méthode du simplexe, c'est à dire. un tableau des coefficients de la fonction objectif et un système d'équations pour les variables correspondantes. Ici "BP" signifie la colonne des variables de base, "Solution" - la colonne des membres de droite des équations du système. La solution n'est pas optimale car il y a des coefficients négatifs dans la ligne z.

itération de méthode simplex 0

							Attitude

Pour améliorer la solution, passons à l'itération suivante méthode du simplexe, on obtient le tableau du simplexe suivant. Pour ce faire, vous devez choisir colonne permissive, c'est à dire. une variable qui sera incluse dans la base à la prochaine itération de la méthode du simplexe. Il est sélectionné par le plus grand coefficient négatif en valeur absolue dans la ligne z (dans le problème maximum) - dans l'itération initiale de la méthode simplex, il s'agit de la colonne x 2 (coefficient -6).

Est alors sélectionné chaîne permissive, c'est à dire. la variable qui sortira de la base à la prochaine itération de la méthode du simplexe. Il est sélectionné par le plus petit rapport de la colonne "Décision" aux éléments positifs correspondants de la colonne de résolution (la colonne "Ratio") - dans l'itération initiale, il s'agit de la ligne s 3 (coefficient 20).

Élément permissif est situé à l'intersection de la colonne de résolution et de la ligne de résolution, sa cellule est mise en évidence, elle est égale à 1. Par conséquent, à la prochaine itération de la méthode simplexe, la variable x 2 remplacera s 1 dans la base. Notez que la relation n'est pas recherchée dans la ligne z ; un tiret "-" y est mis. S'il existe des relations minimales identiques, alors n'importe laquelle d'entre elles est choisie. Si dans la colonne de résolution tous les coefficients sont inférieurs ou égaux à 0, alors la solution du problème est infinie.

Complétons le tableau suivant "Itération 1". Nous l'obtiendrons à partir de la table "Itération 0". Le but des transformations ultérieures est de transformer la colonne de résolution x 2 en une (avec un au lieu de l'élément de résolution et des zéros au lieu des autres éléments).

1) Calcul de la ligne x 2 du tableau "Itération 1". Tout d'abord, nous divisons tous les membres de la ligne résolvante s 3 de la table "Itération 0" par l'élément résolvant (il est égal à 1 dans ce cas) de cette table, nous obtenons la ligne x 2 dans la table Itération 1. Parce que l'élément de résolution dans ce cas est égal à 1, alors la ligne s 3 du tableau "Itération 0" coïncidera avec la ligne x 2 du tableau "Itération 1". Nous avons reçu la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20, le reste des lignes du tableau "Itération 1" sera obtenu à partir de cette ligne et des lignes du tableau "Itération 0" comme suit :

2) Calcul de la ligne z de la table "Itération 1". Au lieu de -6 dans la première ligne (ligne z) de la colonne x 2 du tableau Itération 0, il devrait y avoir 0 dans la première ligne du tableau Itération 1. Pour ce faire, on multiplie tous les éléments de la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20 par 6, on obtient 0 6 0 0 6 120 et on rajoute cette ligne avec la première ligne (z - ligne) du tableau "Itération 0" -4 -6 0 0 0 0, on obtient -4 0 0 0 6 120. Dans la colonne x 2, zéro 0 apparaît, le but est atteint. Les éléments de colonne permissifs x 2 sont surlignés en rouge.

3) Calcul de la ligne s 1 du tableau "Itération 1". A la place 1 dans la ligne 1 de la table "Itération 0", il doit y avoir 0 dans la table "Itération 1". Pour ce faire, on multiplie tous les éléments de la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20 par -1, on obtient 0 -1 0 0 -1 -20 et on ajoute cette ligne avec s 1 - le ligne du tableau "Itération 0" 2 1 1 0 0 64, nous obtenons la ligne 2 0 1 0 -1 44. Dans la colonne x 2 nous obtenons le 0 requis.

4) Calcul de la ligne s 2 du tableau "Itération 1". A la place 3 dans la ligne s 2 de la table "Itération 0", il doit y avoir 0 dans la table "Itération 1". Pour ce faire, on multiplie tous les éléments de la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20 par -3, on obtient 0 -3 0 0 -3 -60 et on ajoute cette ligne avec s 1 - le ligne du tableau "Itération 0" 1 3 0 1 0 72, nous obtenons la ligne 1 0 0 1 -3 12. Dans la colonne x 2, on obtient le 0 requis. La colonne x 2 dans le tableau "Itération 1" a devenir un, il contient un 1 et le reste 0.

Les lignes de la table « Itération 1 » sont obtenues selon la règle suivante :

Nouvelle ligne = Ancienne ligne - (Facteur de colonne de résolution de l'ancienne ligne) * (Nouvelle ligne de résolution).

Par exemple, pour la ligne z nous avons :

Ancienne ligne z (-4 -6 0 0 0 0) - (- 6) * Nouvelle ligne de résolution - (0 -6 0 0 -6 -120) = Nouvelle ligne z (-4 0 0 0 6 120).

Pour les tableaux suivants, le recalcul des éléments du tableau se fait de la même manière, nous l'omettons donc.

méthode simplex itération 1

							Attitude

En admettant la colonne x 1, en résolvant la ligne s 2, s 2 quitte la base, x 1 entre dans la base. Exactement de la même manière, nous obtenons le reste des tables du simplexe jusqu'à ce que nous obtenions une table avec tous les coefficients positifs dans la ligne z. C'est le signe d'une table optimale.

méthode simplex itération 2

							Attitude

La colonne de résolution s 3, la ligne de résolution s 1, s 1 sort de la base, s 3 entre dans la base.

méthode simplex itération 3

							Attitude

Dans la ligne z, tous les coefficients sont non négatifs, par conséquent, une solution optimale est obtenue x 1 = 24, x 2 = 16, z max = 192.

Programmation linéaire est une technique de modélisation mathématique conçue pour optimiser l'utilisation de ressources rares. Le médicament a été utilisé avec succès dans l'armée, l'industrie, l'agriculture, les transports, l'économie, les soins de santé et même dans les sciences sociales. L'utilisation généralisée de cette méthode est également soutenue par des algorithmes informatiques très efficaces qui implémentent cette méthode. Les algorithmes d'optimisation pour d'autres types plus complexes de modèles et de problèmes de recherche opérationnelle (IO), y compris la programmation en nombres entiers, non linéaire et stochastique, sont basés sur des algorithmes de programmation linéaire.

Tâche d'optimisation Est un problème économique et mathématique, qui consiste à trouver la valeur optimale (maximum ou minimum) de la fonction objectif, et les valeurs des variables doivent appartenir à une certaine plage de valeurs admissibles.

Dans sa forme la plus générale, un problème de programmation linéaire s'écrit mathématiquement comme suit :

où X = (x 1 , X 2 , ..., X m ) ; W- plage de valeurs admissibles des variables X 1 , X 2 , ..., X m ;f (X)- fonction objectif.

Pour résoudre le problème d'optimisation, il suffit de trouver sa solution optimale, c'est-à-dire indiquer de telle sorte que pour toute.

Un problème d'optimisation est insoluble s'il n'a pas de solution optimale. En particulier, le problème de maximisation sera insoluble si la fonction objectif f (X) non borné ci-dessus sur l'ensemble admissible W.

Les méthodes de résolution des problèmes d'optimisation dépendent à la fois du type de la fonction objectif f (X), et sur la structure de l'ensemble admissible W... Si la fonction objectif dans le problème est une fonction m variables, alors les méthodes de résolution sont appelées méthodes de programmation mathématique.

Les caractéristiques des problèmes de programmation linéaire sont les suivantes :

indicateur d'optimalité f (X) est une fonction linéaire des éléments de solution X = (x 1 , X 2 , ..., X m ) ;

les conditions restrictives imposées aux solutions possibles prennent la forme d'égalités ou d'inégalités linéaires.

Problème de programmation linéaire la tâche de recherche opérationnelle est appelée, dont le modèle mathématique a la forme:

(2) (3) (4) (5)

Dans ce cas, le système d'équations linéaires (3) et d'inéquations (4), (5), qui détermine l'ensemble admissible de solutions au problème W est appelé système de restrictions problèmes de programmation linéaire, et la fonction linéaire f (X) appelé fonction cible ou alors critère d'optimalité .

Une solution valable est une collection de nombres ( planifier ) X = (X 1 , X 2 , ... , X m ) satisfaire les contraintes du problème. Solution optimale Est un plan dans lequel la fonction objectif prend sa valeur maximale (minimale).

Si le modèle mathématique du problème de programmation linéaire a la forme :

alors ils disent que le problème est présenté dans Forme canonique .

Tout problème de programmation linéaire peut être réduit à un problème de programmation linéaire sous forme canonique. Pour ce faire, dans le cas général, il faut pouvoir réduire le problème de maximisation au problème de minimisation ; passer des contraintes d'inégalité aux contraintes d'égalité et remplacer les variables qui n'obéissent pas à la condition de non-négativité. La maximisation d'une fonction équivaut à la minimisation de la même fonction, prise avec le signe opposé, et vice versa.

La règle pour réduire un problème de programmation linéaire à la forme canonique est la suivante :

si dans le problème d'origine, il est nécessaire de déterminer le maximum d'une fonction linéaire, alors vous devez changer le signe et rechercher le minimum de cette fonction ;

si le côté droit des contraintes est négatif, alors cette contrainte doit être multipliée par -1 ;

s'il y a des inégalités entre les contraintes, alors en introduisant des variables non négatives supplémentaires, elles sont transformées en égalités ;

si une variable X j n'a pas de restrictions de signe, alors il est remplacé (dans la fonction objectif et dans toutes les restrictions) par la différence entre deux nouvelles variables non négatives : X 3 = x 3 + - X 3 - , où X 3 + , X 3 - ≥ 0 .

Exemple 1... En réduisant le problème de programmation linéaire à la forme canonique :

min L = 2x 1 + x 2 - X 3 ; 2x 2 - X 3 5 ; X 1 + x 2 - X 3 -1; 2x 1 - X 2 -3; X 1 0 ; X 2 0 ; X 3 ≥ 0.

On introduit dans chaque équation du système de contraintes les variables de nivellement X 4 , X 5 , X 6 ... Le système s'écrira sous forme d'égalités, et dans les première et troisième équations du système de restrictions les variables X 4 , X 6 sont inscrites dans la partie gauche avec le signe "+", et dans la deuxième équation la variable X 5 saisi avec un signe "-".

2x 2 - X 3 + x 4 = 5 ; X 1 + x 2 - X 3 - X 5 = -1; 2x 1 - X 2 + x 6 = -3; X 4 0 ; X 5 0 ; X 6 ≥ 0.

Les termes libres sous forme canonique doivent être positifs, pour cela on multiplie les deux dernières équations par -1 :

2x 2 - X 3 + x 4 = 5 ; -X 1 - X 2 + x 3 + x 5 = 1 ; -2x 1 + x 2 - X 6 = 3.

Méthode simplex pour résoudre des problèmes de programmation linéaire.

L'algorithme de la méthode du simplexe trouve la solution optimale en considérant un nombre limité de solutions de base admissibles. L'algorithme de la méthode du simplexe commence toujours par une solution de base réalisable, puis essaie de trouver une autre solution de base réalisable qui "améliore" la valeur de la fonction objectif. Ceci n'est possible que si une augmentation de n'importe quelle variable nulle (non fondamentale) conduit à une amélioration de la valeur de la fonction objectif. Mais pour que la variable non fondamentale devienne positive, l'une des variables de base courantes doit être mise à zéro, c'est-à-dire convertir en non basique. Ceci est nécessaire pour que la nouvelle solution contienne exactement m variables de base. Conformément à la terminologie de la méthode du simplexe, la variable zéro sélectionnée est appelée introduit (à la base), et la variable de base supprimée est exclu (à partir de la base).

Deux règles pour le choix des variables introduites et exclues dans la méthode du simplexe seront appelées condition d'optimalité et condition de recevabilité ... Formulons ces règles, et considérons également la séquence d'actions effectuées lors de la mise en œuvre de la méthode du simplexe.

Condition d'optimalité. La variable introduite dans le problème de maximisation (minimisation) est une variable sans base ayant le plus grand coefficient négatif (positif) dans cibler-chaîne de caractères. Si dans cibler-string a plusieurs de ces coefficients, alors le choix de la variable d'entrée est fait arbitrairement. La solution optimale est obtenue lorsqu'en cibler-string, tous les coefficients des variables non fondamentales seront non négatifs (non positifs).

Condition de recevabilité. Dans le problème de maximisation comme dans le problème de minimisation, la variable de base est choisie comme étant la variable exclue, pour laquelle le rapport de la valeur du membre de droite de la contrainte au coefficient positif de la colonne de tête est minimal. S'il existe plusieurs variables de base avec cette propriété, alors le choix de la variable exclue est effectué arbitrairement.

Présentons un algorithme pour résoudre le problème de programmation linéaire pour trouver le maximum en utilisant des tables du simplexe.

F = s 1 x 1 + s 2 x 2 +… + s n x n max

x 1 0, x 2 0,…, x n 0.

1ère étape... Nous introduisons des variables supplémentaires et écrivons le système d'équations résultant et la fonction linéaire sous la forme d'un système étendu.

F – c 1 x 1 –c 2 x 2 -… –c n x n = 0 = c p.

2ème étape. Mise en place d'un premier tableau simplex.

Variables	Variables de base et auxiliaires	membres gratuits (Solution)	Estimé attitude
Variables		membres gratuits (Solution)	Estimé attitude

3ème étape. Nous vérifions le respect du critère d'optimalité - la présence de coefficients négatifs dans la dernière ligne. S'il n'y en a pas, alors la solution est optimale et F * = co, les variables de base sont égales aux coefficients correspondants bj, les variables non fondamentales sont égales à zéro, c'est-à-dire X * = (b 1, b 2,…, bm , 0,…, 0).

4ème étape... Si le critère d'optimalité n'est pas satisfait, alors le plus grand coefficient négatif en valeur absolue de la dernière ligne (estimée) détermine la colonne de résolution s.

Pour déterminer la ligne de résolution, nous calculons les rapports estimés et remplissez la dernière colonne du tableau.

Le rapport estimé de la i-ème ligne est

 si b i et a is ont des signes différents ;

si b i = 0 et а est<0;

si a est = 0 ;

0 si b i = 0 et a est > 0 ;

Dans la colonne des relations de valeur, on trouve l'élément minimum min qui définit la chaîne permissive g.

S'il n'y a pas de minimum, alors le problème n'a pas d'optimum fini I et est insoluble.

A l'intersection de la ligne et de la colonne de résolution se trouve l'élément de résolution a gs.

5ème étape... Nous construisons le tableau suivant. Pour ça

Passons à la troisième étape.

Méthode M Parfois, lors de la résolution de LPP dans la matrice de coefficients avec des systèmes de contraintes inconnus, il n'y a pas de colonnes unitaires à partir desquelles il est possible de composer la matrice unitaire, c'est-à-dire le problème du choix des variables de base se pose, ou la solution originale est invalide. Dans de tels cas, utilisez méthode de base artificielle (M - méthode). Toutes les contraintes où il n'y a pas de variables de base sont introduites variables artificielles. Des variables artificielles sont introduites dans la fonction objectif avec un coefficient (- M) pour les problèmes avec max et avec un coefficient (+ M) pour les problèmes avec min, où M est un nombre positif suffisamment grand... Ensuite, le problème étendu est résolu selon les règles de la méthode du simplexe. Si toutes les variables artificielles sont égales à zéro, c'est-à-dire sont exclus de la base, alors soit une solution optimale au problème d'origine sera obtenue, soit le problème d'origine est résolu plus avant et sa solution optimale est trouvée, soit son indécidabilité est établie. Si au moins une des variables artificielles s'avère non nulle, alors le problème d'origine n'a pas de solution

La méthode universelle pour résoudre les problèmes LP est appelée la méthode du simplexe. Application de cette méthode et de sa modification la plus courante - la méthode simplex à deux phases.

Avec la méthode graphique de résolution des problèmes LP, on choisit en fait dans l'ensemble des sommets appartenant à la frontière de l'ensemble des solutions au système d'inéquations tel un sommet auquel la valeur de la fonction objectif atteint son maximum (minimum). Dans le cas de deux variables, cette méthode est totalement intuitive et permet de trouver rapidement une solution au problème.

S'il y a trois variables ou plus dans le problème, et que dans de vrais problèmes économiques c'est exactement la situation, il est difficile de visualiser le domaine des solutions au système de contraintes. De telles tâches sont résolues en utilisant méthode du simplexe soit par la méthode des améliorations successives. L'idée de la méthode est simple et est la suivante.

Selon une certaine règle, le plan de référence initial est trouvé (quelque sommet de la zone de contrainte). Il est vérifié si le plan est optimal. Si oui, alors le problème est résolu. Sinon, passez à un autre plan amélioré - à un autre sommet. la valeur de la fonction objectif sur ce plan (à ce sommet) est évidemment meilleure que dans le précédent. L'algorithme de transition est effectué à l'aide d'une étape de calcul, qui est commodément écrite sous la forme de tables, appelées tableaux simples ... Puisque le nombre de sommets est fini, alors en un nombre fini d'étapes, nous arrivons à la solution optimale.

Considérons la méthode du simplexe en utilisant un exemple spécifique du problème de l'élaboration d'un plan.

Notez à nouveau que la méthode du simplexe est applicable à la résolution de problèmes canoniques LP réduits à une forme spéciale, c'est-à-dire ayant une base, des membres droits positifs et une fonction objectif exprimée en termes de variables non fondamentales. Si la tâche n'est pas réduite à une forme spéciale, des étapes supplémentaires sont nécessaires, dont nous parlerons plus tard.

Considérons le problème d'un plan de production, ayant préalablement construit un modèle et l'ayant réduit à une forme particulière.

Une tâche.

Pour la fabrication de produits MAIS et DANS l'entrepôt ne peut libérer plus de 80 unités de matières premières. De plus, pour la fabrication du produit MAIS deux unités sont consommées et les produits DANS- une unité de matières premières. Il est nécessaire de planifier la production de sorte que le plus grand profit soit assuré si les produits MAIS il est nécessaire de ne pas fabriquer plus de 50 pièces, et les produits DANS- pas plus de 40 pièces. De plus, le bénéfice de la vente d'un produit MAIS- 5 roubles, et de DANS- 3 roubles.

Construisons un modèle mathématique, notant pour N.-É. 1 nombre de produits A dans le plan, pour N.-É. 2 - nombre de produits DANS... alors le système de restrictions ressemblera à ceci :

x 1 ≤50
x 2 ≤40
2x 1 + x 2 80
x 1 0, x 2 0
5x 1 + 3x 2 → max

Portons le problème sous une forme canonique en introduisant des variables supplémentaires :

x 1 + x 3 = 50
x 2 + x 4 = 40
2x 1 + x 2 + x 5 = 80
x 1 0, x 2 0
5x 1 + 3x 2 → max
-F = -5x 1 - 3x 2 → min.

Ce problème a une forme particulière (avec une base, les membres de droite sont non négatifs). Il peut être résolu en utilisant la méthode du simplexe.

jeétape.Écrire une tâche dans une table simplex. Il existe une correspondance bijective entre le système de contraintes du problème (3.10) et la table du simplexe. Il y a autant de lignes dans le tableau qu'il y a d'égalités dans le système de contraintes, et il y a autant de colonnes que de variables libres. Les variables de base remplissent la première colonne, les variables libres remplissent la première ligne du tableau. La ligne du bas est appelée la ligne d'indice ; elle contient les coefficients des variables de la fonction objectif. Initialement 0 est écrit dans le coin inférieur droit s'il n'y a pas de terme libre dans la fonction ; s'il y en a, nous l'écrivons avec le signe opposé. A cet endroit (dans le coin inférieur droit) se trouvera la valeur de la fonction objectif, qui, lors du passage d'une table à une autre, devrait augmenter en module. Ainsi, notre système de restrictions correspond au tableau 3.4, et nous pouvons passer à l'étape II de la solution.

Tableau 3.4

ligne de base			libre

IIétape... Vérification de l'optimalité du plan de support.

Ce tableau 3.4 correspond au plan de base suivant :

(N.-É. 1 , N.-É. 2 , N.-É. 3 , N.-É. 4 , N.-É. 5) = (0, 0, 50, 40, 80).

Variables libres N.-É. 1 , N.-É. 2 sont 0 ; N.-É. 1 = 0, N.-É. 2 = 0. Et les variables de base N.-É. 3 , N.-É. 4 , N.-É. 5 assumer les valeurs N.-É. 3 = 50, N.-É. 4 = 40, N.-É. 5 = 80 - de la colonne des membres gratuits. Valeur de la fonction objectif :

-F = - 5N.-É. 1 - 3N.-É. 2 = -5 0 - 3 0 = 0.

Notre tâche est de vérifier si un plan de base donné est optimal. pour cela, vous devez afficher la ligne d'index - la ligne de la fonction objectif F.

Différentes situations sont possibles.

1. Dans l'index F-string n'a pas d'éléments négatifs. Cela signifie que le plan est optimal, vous pouvez écrire la solution au problème. La fonction objectif a atteint sa valeur optimale égale au nombre dans le coin inférieur droit pris avec le signe opposé. Nous passons au stade IV.

2. La ligne d'index contient au moins un élément négatif, dont la colonne ne contient aucun élément positif. On conclut alors que la fonction objectif F→ ∞ diminue indéfiniment.

3. La ligne d'index contient un élément négatif avec au moins un élément positif dans sa colonne. Ensuite, nous passons à la prochaine étape III. nous recalculons le tableau, améliorant le plan de base.

IIIétape... Amélioration de la ligne de base.

À partir d'éléments d'index négatifs F-Les lignes choisissent le plus grand en module, appellent la résolution de la colonne correspondante et marquent "".

Pour sélectionner la ligne résolvante, il faut calculer les ratios des éléments de la colonne membre libre seulementÀ positiféléments de colonne permissifs. Choisissez le minimum parmi les relations obtenues. L'élément correspondant, auquel le minimum est atteint, est appelé l'élément résolvant. Nous le soulignerons avec un carré.

Dans notre exemple, l'élément 2 est permissif. La ligne correspondant à cet élément est également appelée résolution (tableau 3.5).

Tableau 3.5

Après avoir choisi l'élément résolvant, on recalcule le tableau selon les règles :

1. Dans le nouveau tableau de même taille que précédemment, les variables de la ligne et de la colonne résolvantes sont permutées, ce qui correspond au passage à une nouvelle base. Dans notre exemple : N.-É. 1 est inclus dans la base, au lieu de N.-É. 5, qui quitte la base et est désormais libre (tableau 3.6).

Tableau 3.6

2. A la place de l'élément résolvant 2, écrivez son nombre inverse ½.

3. Les éléments de la ligne de résolution sont divisés par l'élément de résolution.

4. Les éléments de la colonne de résolution sont divisés par l'élément de résolution et écrits avec le signe opposé.

5. Pour remplir les éléments restants du tableau 3.6, nous recalculons selon la règle du rectangle. Supposons que nous voulions compter l'élément à la position 50.

Nous connectons mentalement cet élément à celui qui résout, trouvons le produit, soustrayons le produit des éléments situés sur l'autre diagonale du rectangle résultant. Nous divisons la différence par l'élément de résolution.

Alors, . On écrit 10 à l'endroit où il y en avait 50. De même :
, , , .

Tableau 3.7

Nous avons un nouveau tableau 3.7, les variables de base sont maintenant les variables (x 3, x 4, x 1). La valeur de la fonction objectif est devenue égale à -200, c'est-à-dire diminué. Pour vérifier l'optimalité de cette solution de base, il faut repasser à l'étape II. Le processus est évidemment fini, les critères d'arrêt sont les points 1 et 2 de l'étape II.

Nous apporterons la solution du problème à la fin. Pour ce faire, vérifiez la ligne d'index et, y voyant un élément négatif -½, appelez la colonne correspondante résolvant et, selon l'étape III, recalculez la table. Après avoir compilé les relations et choisi parmi elles le minimum = 40, nous avons déterminé l'élément résolvant 1. Nous effectuons maintenant le recalcul selon les règles 2-5.

Tableau 3.8

Après avoir recalculé la table, nous nous assurons qu'il n'y a pas d'éléments négatifs dans la ligne d'index, par conséquent, le problème est résolu, le plan de base est optimal.

IVétape... Rédaction de la solution optimale.

Si la méthode simplex s'est arrêtée conformément au point 1 de l'étape II, la solution du problème est écrite comme suit. Les variables de base prennent respectivement les valeurs de la colonne membre libre. Dans notre exemple N.-É. 3 = 30, N.-É. 2 = 40, N.-É. 1 = 20. Les variables libres sont 0, N.-É. 5 = 0, N.-É. 4 = 0. La fonction objectif prend la valeur du dernier élément de la colonne des membres libres de signe opposé : - F = -220 → F= 220, dans notre exemple la fonction a été examinée pour min, et initialement F→ max, donc en fait le signe a changé deux fois. Alors, N.-É.* = (20, 40, 30, 0, 0), F* = 220. Réponse au problème :

Il faut inclure 20 produits du type MAIS, 40 produits de type B, tandis que le bénéfice sera maximum et sera égal à 220 roubles.

À la fin de cette section, nous présentons un schéma fonctionnel de l'algorithme de la méthode du simplexe, qui répète exactement les étapes, mais, peut-être, pour certains lecteurs, il sera plus pratique à utiliser, car les flèches indiquent une direction claire de l'action .

Les liens au-dessus des cases de l'organigramme indiquent à quelle étape ou sous-clause appartient le groupe de transformation correspondant. la règle pour trouver le plan de référence initial sera formulée à la clause 3.7.

Un exemple. Résolvez le problème LP suivant sous forme canonique en utilisant la méthode du simplexe.
f (x) = x 1 + 9x 2 + 5x 3 + 3x 4 + 4x 5 + 14x 6 → min
x 1 + x 4 = 20
x 2 + x 5 = 50
x 3 + x 6 = 30
x 4 + x 5 + x 6 = 60
x i 0, i = 1, ..., 6
Ils disent qu'un problème LP a une forme canonique si toutes les contraintes (à l'exception des conditions de non-négativité des variables) ont la forme d'égalités, et tous les termes libres sont non négatifs. Nous avons donc un problème sous forme canonique.
L'idée derrière la méthode du simplexe est la suivante. Tout d'abord, vous devez trouver un sommet (initial) du polyèdre des solutions réalisables (solution de base réalisable initiale). Ensuite, vous devez vérifier l'optimalité de cette solution. Si elle est optimale, alors la solution a été trouvée ; sinon, passez à un autre sommet du polytope et vérifiez à nouveau l'optimalité. Compte tenu de la finitude des sommets du polyèdre (une conséquence de la finitude des restrictions du problème LP) en un nombre fini de "pas" nous trouverons le point minimum ou maximum requis. Il est à noter qu'en passant d'un sommet à un autre, la valeur de la fonction objectif diminue (dans le problème pour le minimum) ou augmente (dans le problème pour le maximum).
Ainsi, l'idée de la méthode du simplexe repose sur trois propriétés du problème LP.
Solution. Pour trouver la solution de base réalisable initiale, c'est-à-dire pour déterminer les variables de base, le système (5.6) doit être réduit à une forme "diagonale". En appliquant la méthode de Gauss (méthode d'élimination successive des inconnues), on obtient de (5.6) :
x 2 + x 1 + x 3 = 40
x 4 + x 1 = 20
x 5 -x 1 -x 3 = 10
x 6 + x 3 = 30
Par conséquent, les variables de base sont x 2, x 4, x 5, x 6, nous leur attribuons des valeurs égales aux membres libres des chaînes correspondantes : x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,... Variables x 1 et x 3 ne sont pas basiques : x 1 = 0, x 3 = 0.
Construisons la solution de base admissible initiale
x 0 = (0,40,0,20,10,30) (5,9)
Pour vérifier l'optimalité de la solution trouvée x 0 il est nécessaire d'exclure les variables de base de la fonction objectif (en utilisant le système (5.8)) et de construire un tableau simplex spécial.
Après avoir éliminé les variables, la fonction objectif peut être commodément écrite comme :
f (x) = -7x 1 - 14x 3 +880 (5,10)
Maintenant, en utilisant (5.8) - (5.10), nous composons une table simplex initiale :

La ligne zéro contient les coefficients de signe opposé des variables correspondantes pour la fonction objectif. Critère d'optimalité (pour le problème de trouver un minimum) : solution de base admissible ( x 0) est optimale si la ligne zéro ne contient pas un seul nombre strictement positif (sans compter la valeur de la fonction objectif (880)). Cette règle s'applique également aux itérations suivantes (tableaux). Les éléments de la ligne zéro seront appelés estimations de colonne.
Donc la solution de base admissible initiale (5.9) n'est pas optimale : 7>0, 14>0 .
La colonne zéro contient les valeurs des variables de base. Ils doivent être non négatifs (voir équation (5.7)). De la première à la quatrième ligne, les coefficients des variables du système (5.8) sont écrits.
Comme x 0 n'est pas optimal, alors vous devez aller à un autre sommet du polyèdre des solutions réalisables (construire un nouveau b.d.). Pour ce faire, vous devez trouver le pivot et effectuer une certaine transformation (transformation simplex).
Tout d'abord, nous trouvons l'élément de tête du tableau, qui se situe à l'intersection de la colonne de tête (la colonne avec le score positif le plus élevé) et de la ligne de tête (la ligne correspondant au rapport minimum des éléments de la colonne zéro au éléments correspondants (strictement positifs) de la colonne de tête).
Dans le tableau 1, la première colonne est la troisième colonne et la première ligne est la quatrième. (min (40/1,30/1) = 30/1) sont indiqués par des flèches, et l'élément de tête est indiqué par un cercle. L'hôte indique que la variable sous-jacente x 6 doit être remplacé par un non basique x 3... Ensuite, les nouvelles variables de base seront x 2, x 3, x 4, x 5,, et non basiques - x 1, x 6,... Cela signifie une transition vers un nouveau sommet du polyèdre des solutions réalisables. Pour trouver les valeurs de coordonnées de la nouvelle solution de base réalisable x 00 vous devez construire une nouvelle table simplex et y effectuer des transformations élémentaires :
mais) diviser tous les éléments de la ligne principale par l'élément principal, transformant ainsi l'élément principal en 1 (pour la simplicité des calculs);
b) en utilisant l'élément de tête (égal à 1), transformez tous les éléments de la colonne de tête en zéros (similaire à la méthode d'élimination des inconnues);
En conséquence, dans la colonne zéro, les valeurs des nouvelles variables de base sont obtenues x 2, x 3, x 4, x 5,(voir tableau 2) - composants de base du nouveau sommet x 00(composants non essentiels x 1 = 0, x 6 = 0,).

Comme le montre le tableau 2, la nouvelle solution de base x 00 = (0.10,30,20,40,0) non optimale (la ligne zéro a un score non négatif de 7). Par conséquent, avec l'élément pivot 1 (voir tableau 2), nous construisons un nouveau tableau simplex, c'est-à-dire construire une nouvelle solution de base réalisable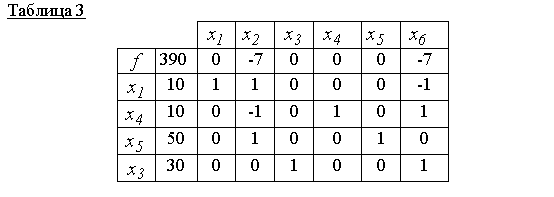

Le tableau 3 correspond à la solution de base admissible x 000 = (10,0,30,10,50,0) et c'est optimal, car il n'y a pas de notes positives dans la ligne zéro. donc f (x 000) = 390 est la valeur minimale de la fonction objectif.
Réponse: x 000 = (10, 0, 30, 10, 50, 0)- note minimale, f (x 000) = 390.

Problème de programmation linéaire conditionnellement standard

Vous devez effectuer les tâches suivantes dans l'ordre indiqué.

Trouvez le plan optimal pour le problème direct :
a) méthode graphique ;
b) la méthode du simplex (il est recommandé d'utiliser la méthode des bases artificielles pour construire le plan de référence initial).
Construire un problème dual.
Trouver le plan optimal du problème dual à partir de la solution graphique de la droite en utilisant les conditions de jeu complémentaires.
Trouvez le plan optimal pour le problème dual par le premier théorème de dualité, en utilisant le tableau du simplexe final obtenu en résolvant le problème direct (voir élément 1b). Vérifiez l'énoncé « les valeurs des fonctions objectifs d'une paire de problèmes doubles coïncident sur leurs solutions optimales ».
Résoudre le problème dual par la méthode du simplexe, puis, en utilisant la table du simplexe finale du problème dual, trouver le plan optimal du problème direct selon le premier théorème de dualité. Comparez le résultat avec le résultat obtenu par la méthode graphique (voir point 1a).
Trouvez la solution entière optimale :
a) méthode graphique ;
b) Par la méthode de Gomori.
Comparer les valeurs des fonctions de solutions entières et non entières

Questions pour la maîtrise de soi

Comment est construite une table simplex ?
Comment le changement de base est-il reflété dans le tableau ?
Formuler un critère d'arrêt pour la méthode du simplexe.
Comment organiser le recalcul de table ?
Avec quelle ligne est-il pratique de commencer à recalculer la table ?

Pour permettre à l'applet de s'exécuter sur votre ordinateur, vous devez procéder comme suit : cliquez sur Démarrer > Panneau de configuration > Programmes > Java. Dans la fenêtre du panneau de configuration Java, sélectionnez l'onglet Sécurité, cliquez sur le bouton Modifier la liste des sites, le bouton Ajouter et insérez le chemin d'accès à cette page à partir de la barre d'adresse du navigateur dans le champ libre. Ensuite, nous appuyons sur les boutons OK, après quoi nous redémarrons l'ordinateur.

Pour lancer l'applet, cliquez sur le bouton "Simplex". Si le bouton "Simplex" n'est pas visible au-dessus de cette ligne, alors Java n'est pas installé sur l'ordinateur.

Après avoir cliqué sur le bouton "Simplex", la première fenêtre s'affiche pour saisir le nombre de variables et le nombre de restrictions de tâches pour la méthode simplex.

Après avoir cliqué sur le bouton « ok », une fenêtre s'affiche pour saisir le reste des données de la tâche pour la méthode simplex : le mode d'affichage (fractions décimales ou fractions ordinaires), le type de critère de tâche min ou max, la saisie des coefficients de la fonction objectif et les coefficients du système de contraintes avec les signes "≤", " ≥ "ou" = ", les restrictions de la forme х i ≥ 0 n'ont pas besoin d'être saisies, les prend en compte dans son algorithme.

Après avoir cliqué sur le bouton "Résoudre", une fenêtre avec les résultats de la résolution du problème sur .La fenêtre se compose de deux parties, dans la partie supérieure il y a un champ de texte contenant une description de la réduction du problème original à la forme canonique, qui est utilisée pour composer le premier tableau simplex. Au bas de la fenêtre, dans un volet à onglets, il y a des tableaux simplex de chaque itération avec une petite zone de texte en bas indiquant la colonne de résolution, les lignes de résolution et d'autres informations, faisant du programme un didacticiel. Dans l'onglet avec le (dernier) tableau optimal, la solution optimale obtenue au problème est affichée dans le champ de texte.

Veuillez envoyer les erreurs et commentaires constatés sur l'applet à [email protégé] ou appelez le 8 962 700 77 06, nous vous en serons très reconnaissants.

Programme de la méthode M

Le programme pour résoudre le problème de transport

Voici une solution manuelle (pas une applet) de deux problèmes par une méthode simplex (similaire à une solution d'applet) avec des explications détaillées afin de comprendre l'algorithme de résolution de problèmes. Le premier problème ne contient que des signes d'inégalité "≤" (un problème avec une base initiale), le second peut contenir des signes "≥", "≤" ou "=" (un problème avec une base artificielle), ils sont résolus de différentes manières .

Méthode simplex, résolution d'un problème avec une base initiale

1)Méthode simplex pour un problème avec une base initiale (tous les signes d'inégalité-contraintes "≤").

Écrivons la tâche dans canonique forme, c'est-à-dire les contraintes d'inégalité peuvent être réécrites comme des égalités en ajoutant bilan variables :

Ce système est un système à base (base s 1, s 2, s 3, chacun d'eux est inclus dans une seule équation du système de coefficient 1), x 1 et x 2 sont des variables libres. Les problèmes résolus à l'aide de la méthode du simplexe doivent avoir les deux propriétés suivantes :
- le système de contraintes doit être un système d'équations à base ;
- les termes libres de toutes les équations du système doivent être non négatifs.

Le système résultant est un système avec une base et ses termes libres sont non négatifs ; par conséquent, la méthode du simplexe peut être appliquée. Composons le premier tableau du simplexe (Itération 0), c'est-à-dire un tableau des coefficients de la fonction objectif et un système d'équations pour les variables correspondantes. Ici "BP" signifie la colonne des variables de base, "Solution" - la colonne des membres de droite des équations du système. La solution n'est pas optimale car il y a des coefficients négatifs dans la ligne z.

itération 0

PA	Solution	Attitude

Pour améliorer la solution, passons à l'itération suivante et obtenons le tableau simplex suivant. Pour ce faire, vous devez choisir colonne permissive, c'est à dire. une variable qui sera incluse dans la base à la prochaine itération. Il est sélectionné par le plus grand coefficient négatif en valeur absolue dans la ligne z (dans le problème maximum) - dans l'itération initiale, il s'agit de la colonne x 2 (coefficient -6).

Est alors sélectionné chaîne permissive, c'est à dire. la variable qui sortira de la base à l'itération suivante. Il est sélectionné par le plus petit rapport de la colonne "Décision" aux éléments positifs correspondants de la colonne de résolution (la colonne "Ratio") - dans l'itération initiale, il s'agit de la ligne s 3 (coefficient 20).

Élément permissif est à l'intersection de la colonne de résolution et de la ligne de résolution, sa cellule est mise en évidence, elle est égale à 1. Ainsi, à l'itération suivante, la variable x 2 remplacera s 3 dans la base. Notez que la relation n'est pas recherchée dans la ligne z ; un tiret "-" y est mis. S'il existe des relations minimales identiques, alors n'importe laquelle d'entre elles est choisie. Si dans la colonne de résolution tous les coefficients sont inférieurs ou égaux à 0, alors la solution du problème est infinie.

2) Calcul de la ligne z de la table "Itération 1". Au lieu de -6 dans la première ligne (ligne z) de la colonne x 2 du tableau Itération 0, il devrait y avoir 0 dans la première ligne du tableau Itération 1. Pour ce faire, on multiplie tous les éléments de la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20 par 6, on obtient 0 6 0 0 6 120 et on ajoute cette ligne avec la première ligne (z - ligne) de le tableau "Itération 0" -4 -6 0 0 0 0, on obtient -4 0 0 0 6 120. Le zéro 0 apparaît dans la colonne x 2, l'objectif est atteint. Les éléments de colonne permissifs x 2 sont surlignés en rouge.

3) Calcul de la ligne s 1 du tableau "Itération 1". A la place 1 dans la ligne 1 de la table "Itération 0", il doit y avoir 0 dans la table "Itération 1". Pour ce faire, on multiplie tous les éléments de la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20 par -1, on obtient 0 -1 0 0 -1 -20 et on ajoute cette ligne avec s 1 - la ligne du tableau "Itération 0" 2 1 1 0 0 64, nous obtenons la ligne 2 0 1 0 -1 44. Dans la colonne x 2, nous obtenons le 0 requis.

4) Calcul de la ligne s 2 du tableau "Itération 1". A la place 3 dans la ligne s 2 de la table "Itération 0", il doit y avoir 0 dans la table "Itération 1". Pour ce faire, on multiplie tous les éléments de la ligne x 2 du tableau "Itération 1" 0 1 0 0 1 20 par -3, on obtient 0 -3 0 0 -3 -60 et on ajoute cette ligne avec s 2 - le ligne du tableau "Itération 0" 1 3 0 1 0 72, nous obtenons la ligne 1 0 0 1 -3 12. Dans la colonne x 2, on obtient le 0 souhaité. La colonne x 2 dans le tableau "Itération 1" est devenue une , il contient un 1 et le reste 0.

Les lignes de la table « Itération 1 » sont obtenues selon la règle suivante :

Nouvelle ligne = Ancienne ligne - (Facteur de colonne de résolution de l'ancienne ligne) * (Nouvelle ligne de résolution).

Par exemple, pour z -string nous avons :

Ancienne chaîne Z (-4 -6 0 0 0 0)
- (- 6) * Nouvelle chaîne de résolution - (0-6 0 0 -6 -120)
= Nouvelle ligne z(-4 0 0 0 6 120) .

Pour les tableaux suivants, le recalcul des éléments du tableau se fait de la même manière, nous l'omettons donc.

itération 1

						Solution	Attitude

Itération 2

						Solution	Attitude

La colonne de résolution s 3, la ligne de résolution s 1, s 1 sort de la base, s 3 entre dans la base.

Itération 3

						Solution	Attitude

Dans la ligne z, tous les coefficients sont non négatifs, par conséquent, une solution optimale est obtenue x 1 = 24, x 2 = 16, z max = 192.

Méthode simplex, résoudre un problème avec une base artificielle

2) Résolvons le problème avec une base artificielle (au moins un signe d'inégalité-contraintes "≥" ou "=").

Écrivons le problème sous forme canonique (sous la forme d'un système d'équations, ce qui nécessite la méthode du simplexe), pour cela on introduit deux variables x 3 0 et x 4 0 on obtient :

Le système de contraintes n'offre qu'une seule variable de base admissible x 4, seulement elle n'est incluse que dans une seule équation de la troisième avec un coefficient de 1, donc on ajoute les variables artificielles R 1 0 et R 2 0 aux première et deuxième équations Les équations-contraintes doivent être un système avec une base, c'est-à-dire dans chaque équation il doit y avoir une variable de coefficient 1, qui n'est incluse que dans une seule équation du système, dans notre cas il s'agit de R 1, R 2 et x 4. Nous avons le soi-disant problème M :

Ce système est un système avec une base dans laquelle R 1, R 2 et x 4 sont des variables de base, et x 1, x 2 et x 3 sont des variables libres, les termes libres de toutes les équations sont non négatifs. Par conséquent, la méthode du simplexe peut être utilisée pour résoudre le problème. Écrivons la table simplex initiale :

itération 0

	Solution	Attitude
-16

Ajout de la ligne « Évaluation » au tableau pour les tâches avec une base artificielle. Il est obtenu en sommant les coefficients correspondants des lignes avec les variables artificielles (R) de signe opposé. Il sera présent dans le tableau tant qu'au moins une des variables artificielles est dans la base. Par le plus grand coefficient négatif modulo de la ligne "Score", la colonne de résolution est déterminée alors qu'elle est dans le tableau. Lorsque la ligne "Score" quitte le tableau (il n'y a pas de variables artificielles dans la base), la colonne de résolution sera déterminée par la ligne z, comme dans le problème avec la base initiale. Dans ce tableau, la colonne résolvante est x 2, elle est sélectionnée selon la plus grande estimation modulo négative (-7). La ligne de résolution R 2 est sélectionnée selon le plus petit rapport de la colonne "Décision" aux éléments positifs correspondants de la colonne de résolution, comme dans le problème sans variables artificielles. Cela signifie qu'à l'itération suivante, la variable x 2 passera de libre à basique, et la variable R 2 de basique à libre. Écrivons le tableau simplex suivant :

Colonne permissive x 1, ligne permissive R 1, R 1 quitte la base, x 1 entre dans la base. Après cela, il ne reste plus de variables artificielles dans la base, il n'y a donc pas de ligne « Evaluation » dans le tableau suivant :

itération 2

							Solution	Attitude

Ensuite, la colonne de résolution est sélectionnée par la ligne z. Dans la ligne z, tous les coefficients sont non négatifs à l'exception du coefficient du mannequin R 1, qui n'affecte pas l'optimalité lorsque le mannequin est hors de la base. Par conséquent, une solution optimale est obtenue x 1 = 6/5 ; x 2 = 3/5 ; zmax = 72/5.

Cas particuliers de la méthode simplex

1) Lorsqu'une droite (si l'on considère un problème de programmation linéaire à deux dimensions, et dans le cas général un hyperplan) représentant la fonction objectif est parallèle à la droite (hyperplan) correspondant à l'une des contraintes d'inégalité (qui est satisfaite au point optimal comme une égalité exacte), la fonction objectif prend un et est également la valeur optimale sur un ensemble de points de la frontière de la région des solutions réalisables. Ces solutions sont appelées solutions optimales alternatives... La disponibilité de solutions alternatives peut être déterminée par la table simplex optimale. Si la ligne z du tableau optimal contient des coefficients nuls de variables non fondamentales, alors il existe des solutions alternatives.

2) Si dans la colonne de résolution de la table du simplexe tous les coefficients sont inférieurs ou égaux à zéro, alors la ligne de résolution ne peut pas être sélectionnée, dans ce cas la solution est non bornée.

3) Si les contraintes d'un problème de programmation linéaire sont incohérentes (c'est-à-dire qu'elles ne peuvent pas être exécutées simultanément), alors le problème n'a pas de solutions réalisables. Cette situation ne peut se produire si toutes les inégalités qui composent le système de contraintes sont de type "≤" avec des membres droits non négatifs, puisque dans ce cas, des variables supplémentaires peuvent constituer une solution réalisable. Pour les autres types de contraintes, des variables artificielles sont utilisées. Si le problème a une solution, alors dans le tableau optimal de la base il n'y a pas de variables artificielles (R i). S'ils sont là, alors le problème n'a pas de solutions.