Simplex meetodi algoritm. Simplexi meetod ZLP lahendamisel. Tingimuslikult tavaline lineaarne programmeerimisülesanne

Kui teil on vaja lahendada lineaarse programmeerimise ülesande, kasutades Simplex tabelid, siis meie võrguteenus annab teile suure abi. Sümbolimeetod hõlmab järjestikuseid otsinguid kõigi kehtivate väärtuste tippude otsimiseks, et leida tipu, kus funktsioon võtab äärmusliku väärtuse. Esimeses etapis on mõningane lahendus, mis parandab iga järgneva etapi. Seda lahendust nimetatakse aluseks. Tutvustame tegevuste järjestust lineaarse programmeerimise probleemide lahendamisel:

Esimene samm. Esimese tabeli tabelis on vaja vaadata veeru vaba liikmetega. Kui selles on negatiivseid elemente, siis on vaja teise sammu liikuda, siis ei ole viiendani.

Teine samm. Teises etapis on vaja kindlaks määrata, milline muutuja katsetatakse põhjal ja mida sisse lülitada, et lihtsustada Simplex tabelit. Selleks vaatame veeru tasuta liikmetega ja leida selles negatiivne element. Negatiivse elemendiga stringi nimetatakse võõrustajaks. Selles leiame maksimaalse mooduli veerg vastava negatiivne element - ori. Kui vaba liikmete hulgas on negatiivseid väärtusi ja vastavas liinil ei ole, siis ei ole selline tabelis lahendusi. Vaba liikmete kolonnis asuv varieeruv varieeruv, mis asub vabade liikmete veerus, jäetakse alusest ja muutuja, mis vastab juhtivale stseenile, on aluseks.

Tabel 1.

Põhilised muutujad	Tasuta liikmed piirangutes	Nebase muutujad
Põhilised muutujad	Tasuta liikmed piirangutes	x 1	x 2	...	x L.	...	x N.
x n + 1	b 1.	a 11.	12.	...	1 l.	...	1n.
x n + 2	b 2.	a 21.	a 22.	...	2 l	...	2N.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n + r	b2.	r1	r2.	...	rL	...	rn.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n + m	b M.	m1.	m2.	...	ml.	...	mN.
F (x) max	F 0.	-C 1.	-C 2.	...	-C 1.	...	-C N.

Kolmas samm. Kolmandas etapis tõlkime kogu simplex tabeli spetsiaalsetele valemitele, neid valemeid saab näha kasutades.

Neljas samm. Kui pärast vaba liikmete veerus ümberarvutamist jäi eitanud elemendid, siis pöördume esimese sammu poole, kui selliseid ei ole, siis viiendani.

Viies samm. Kui olete viies samm jõudnud, leidsime, et lubatav lahendus. Kuid see ei tähenda, et see on optimaalne. See on optimaalne ainult siis, kui kõik F-reas olevad elemendid on positiivsed. Kui see nii ei ole, on vaja lahendust parandada, mille jaoks leiame järgmise algoritmi juhtiv string ja veerg järgmise ümberarvumise jaoks. Esialgu leiame F-liinil minimaalse negatiivse numbri, välja arvatud funktsiooni väärtus. Veerg selle numbriga ja on juhtpositsioon. Juhendatava liini leidmiseks leiame sobiva vaba liikme ja elemendi suhe plii kolonnist, tingimusel et need on positiivsed. Minimaalne suhe võimaldab teil määrata Master String. Re-läbida tabel valemite, st Mine sammu 3.

Siin käsitsi (mitte applet) antakse lahendus kahe ülesanded simplex meetodil (sarnane apleti lahendus) üksikasjalikud selgitused, et mõista probleem lahendamise algoritmi simplex-meetod. Esimene ülesanne sisaldab ainult ebavõrdsuse tähiseid ainult "≤" (esialgse alusega ülesanne), teine \u200b\u200bvõib sisaldada märke "≥", "≤" või "\u003d" (kunstliku alusega ülesanne), need lahendatakse erinevalt.

Simplex-meetod, ülesande lahendamine esialgse alusega

1)Simplex meetodesialgse aluse ülesande täitmiseks (kõik ebavõrdsuse tunnused "≤").

Me kirjutame ülesande B. kanooniline Vorm, s.o. Ebavõrdsuse piirangud kirjutab ümber võrdsuste vormis tasakaal Muutujad:

See süsteem on süsteemi alusega (alus S 1, S 2, S 3, igaüks neist siseneb ainult ühe võrrandi süsteemi koefitsiendiga 1), x 1 ja x 2 - vaba muutujaid. Ülesanded, kui lahendamisel simpleks-meetodi rakendatakse, peaks olema järgmised kaks omadust: - piirangute süsteem peaks olema võrdsete süsteemide süsteemiga; - Süsteemi kõigi võrrandite toetatavad tingimused peavad olema mitte-negatiivsed.

Saadud süsteem - süsteemi aluse ja selle vaba liikmed on mittegatiivsed, nii et saate taotleda simplex meetod. Avage probleemi lahendamiseks esimene simplex tabel (iteratsioon 0) Simplex meetod. Sobivate muutujatega sihtfunktsioonide koefitsientide ja võrrandite süsteemi tabel. Siin tähendab "BP" põhiliste muutujate veeru, "lahendus" - süsteemi võrrandite parema osa veerus. Otsus ei ole optimaalne, sest Z-liinis on negatiivsed koefitsiendid.

simplex-meetodi iteratsiooni 0

							Suhtumine

Lahenduse parandamiseks pöördume järgmise iteratsiooni poole simplex meetodMe saame järgmise simplex tabeli. Selleks peate valima lubav veerg. Muutuja, mis sisestab Simplexi meetodi järgmisel iteratsiooni aluse. See on valitud suurima mooduli negatiivse koefitsiendi Z-rida (maksimaalse probleemi) - esialgse iteratsiooni Simplex meetod, see veerg X2 (koefitsient -6).

Seejärel valitud eraldusvõimega string. Muutuja, mis vabastatakse Simplexi meetodi järgmisel iteratsiooni alusel. See valitakse veeru väikseim suhtumine resolutsioonikolonni vastavatele positiivsele elementidele (kolonn "suhe") - esialgses iteratsioonis on see string S 3 (koefitsient 20).

Elementide lubamine See on resolutsioonikolonni ristumiskohas ja resolutsioon, selle rakk isoleeritakse värviga, see on 1. Seega, Simplexi meetodi järgmisel iteratsioonis asendatakse muutuja X2 aluse S 1-s. Pange tähele, et Z-rida suhtumine ei otsi, seal on kriips "-". Juhul kui on olemas sama minimaalne suhe, siis ükskõik milline neist on valitud. Kui kõik koefitsiendid on eraldusvõime veerus väiksemad või võrdsed, on probleemide lahendamine lõpmatu.

Täitke järgmine tabel "Iteration 1". Me saame selle "iteratsiooni 0" tabelist. Eesmärkide edasiste muutuste eesmärk on muuta eraldusvõime veerg X2 üheks (koos ühiku asemel eraldusvõime elemendi ja nulli asemel teiste elementide asemel).

1) arvutamine string x 2 tabel "iteratsioon 1". Kõigepealt jagame kõik resolutsioonis S 3 tabelit "iteratsiooni 0" resolutsioonile elemendile (see on 1 sel juhul) selle tabeli, saame stringi x 2 "iteratsiooni 1" tabelis. Sest Sellisel juhul lahendamisel element on 1, siis tabeli "iteratsiooni 0" liin S3 langeb kokku "iteratsiooni 1" tabeli rida x 2-ga. Line x 2 tabelid "Iteration 1" Meil \u200b\u200bon 0 1 0 0 1 20, ülejäänud read "iteratsiooni 1" tabel saab selle joone ja "iteratsiooni 0" stringid järgmiselt:

2) Z-rida tabeli "iteratsiooni arvutamine 1". Alas -6 esimeses real (Z-rida) tabeli X 2 veerus X2 veerus "iteratsioon 0" peab olema "iteratsiooni 1" esimene rida. Selleks, kõik elemendid string x 2 tabel "iteratsioon 1" 0 1 0 0 1 20 korrutada 6, saame 0 6 0 0 6 120 ja panna see string esimese rea (Z-liin) tabel "iteratsioon 0 "-4 -6 0 0 0 0, saame -4 0 0 0 6 120. veerus X2 2 ilmus null 0, eesmärk saavutatakse. Lahendamise elemendid veerg X2 on esile tõstetud punaselt.

3) stringi S 1 tabeli "iteratsiooni arvutamine 1". Alas 1 s 1 rida "iteratsiooni 0" tabel peab olema 0 "iteratsiooni 1" tabelis. Selleks kõik elemendid string x 2 tabel "iteratsioon 1" 0 1 0 0 1 20 korrutada -1, saame 0 -1 0 -1 -1 -20 ja panna see string s 1 - liin tabelis "Iteratsiooni 0" 2 1 1 0 0 64, saame stringi 2 0 1 0 -1 44. Kolonnis X 2, vajalik 0 saadakse.

4) stringi S 2 tabeli "iteratsiooni arvutamine 1". Kohas 3 S 2 rida "iteratsiooni 0" tabelis peaks olema 0 "iteratsiooni 1" tabelis. Selleks, kõik elemendid string x 2 tabel "iteratsiooni 1" 0 1 0 0 1 20 korrutada -3, saame 0 -3 0 0-3 -60 ja panna see string S 1-line tabelis "Iteration 0" 1 3 0 1 0 72, saame stringi 1 0 0 1 -3 12. Kolonnis X2 soovitud 0 saadakse. Veerg X 2 "iteratsiooni 1" tabelis sai üheks, See sisaldab ühte 1 ja ülejäänud 0.

Ridade "iteratsiooni 1" tabel saadakse vastavalt järgmisele reeglile:

Uus rida \u003d vana string - (vana liini lubava veeru koefitsient) * (uus lubav string).

Näiteks Z-rida jaoks on meil:

Vana Z-rida (-4 -6 0 0 0 0) - (- 6) * Uus võimaldav string - (0 -6 0 0 -6 -120) \u003d uus Z-line (-4 0 0 6 120).

Järgmiste tabelite puhul tehakse tabeli elementide ümberarvutamine sarnaselt, nii et me jätkasime seda.

simplex-meetodi iteratsiooni 1

							Suhtumine

Resolutsioonis X1 1, S 2 stringi lahutamine, S2 jätab aluse, X 1 siseneb aluse. Täiesti sarnane teiste simplex tabelitega, kuni tabel on saadud kõigi positiivsete koefitsientide Z-reas. See on märk optimaalsest tabelist.

simplex-meetodi iteratsiooni 2

							Suhtumine

Resolutsioonis kolonn S 3, stringi S 1, S 1 lahustub aluse, S 3 siseneb aluse.

simplex-meetodi iteratsiooni 3

							Suhtumine

Z-reas kõik koefitsiendid on mitte-negatiivsed seetõttu optimaalne lahus x 1 \u003d 24, x 2 \u003d 16, z max \u003d 192 saadi.

Lineaarne programmeerimine - See on matemaatilise modelleerimise meetod, mille eesmärk on optimeerida piiratud ressursside kasutamist. LP kasutatakse edukalt sõjalises valdkonnas, tööstuses, põllumajanduses, transporditööstuses, majanduses, tervishoiusüsteemis ja isegi sotsiaalteadustes. Selle meetodi laialdast kasutamist toetavad ka väga tõhusad arvuti algoritmid, mis seda meetodit rakendavad. Lineaarsete programmeerimisalgoritmide puhul põhinevad optimeerimise algoritmid teistele, keerukamatele mudelitele ja operatsioonide uuringutele (IO), sealhulgas täisarv, mittelineaarsed ja stohhastilised programmeerimine.

Optimeerimise ülesanne - See on majanduslik ja matemaatiline ülesanne, mis seisneb optimaalse (maksimaalse või minimaalse) väärtuse leidmisel sihtfunktsiooni ja muutujate väärtused peavad kuuluma mõnele lubatud väärtuste piirkonda.

Kõige üldisem vorm on lineaarne programmeerimise ülesanne matemaatiliselt kirjutatud järgmiselt:

kus X \u003d (x 1 , X. 2 ..., x n. ) ; W. - muutujate lubatud väärtuste ala x. 1 , X. 2 ..., x n. ;f (x) - Sihtfunktsioon.

Optimeerimise probleemi lahendamiseks piisab selle optimaalse lahenduse leidmiseks, st Määrake selline mis tahes.

Optimeerimise ülesanne on juhtitav, kui tal ei ole optimaalset lahendust. Eelkõige on maksimeerimisülesanne võimatu, kui sihtfunktsioon f (x) ei piirdu lubatud komplekti peal W..

Optimeerimisülesannete lahendamise meetodid sõltuvad sihtfunktsiooni tüübist f (x)ja lubatud komplekti struktuurist W.. Kui ülesande sihtfunktsioon on funktsioon n. Muutujad, seejärel meetodeid lahenduste nimetatakse matemaatiliste programmide meetodite.

Lineaarsete programmeerimisülesannete iseloomulikud tunnused on järgmised:

optimaalsuse indikaator f (x) kujutab lahenduse elementide lineaarset funktsiooni X \u003d (x 1 , X. 2 ..., x n. ) ;

võimalike lahenduste piiravatel tingimustel on lineaarsete võrdõiguslikkuse või ebavõrdsuse liik.

Lineaarne programmeerimisülesanne Õppimise ülesannete ülesanne on matemaatiline mudel, mille kujul on:

(2) (3) (4) (5)

Sel juhul süsteem lineaarne võrrandid (3) ja ebavõrdsuse (4), (5), mis määrab lubatud lahendusi lahendusi W., kutsus süsteemi piirangud Lineaarsed programmeerimisülesanded ja lineaarne funktsioon f (x) kutsus sihtfunktsioon või optimaalsuse kriteerium .

Lubatud lahendus - See on numbrite kogum ( plaanima ) X. = (x. 1 , x. 2 , ... , x. n. ) ülesande piirangute rahuldamine. Optimaalne lahendus - See on plaan, kus sihtmärk on maksimaalne (minimaalne) väärtus.

Kui matemaatiline mudel lineaarne programmeerimisprobleem on:

nad ütlevad, et ülesanne on esitatud kanooniline vorm .

Igasugune lineaarse programmeerimise ülesanne võib vähendada lineaarse programmeerimisülesandega kanoonilises vormis. Selleks peate üldiselt suutma vähendada minimeerimise probleemi maksimeerimisülesannet; Kontroll piirangute ebavõrdsuse piirangute võrdsuse ja asendada muutujad, mis ei kuulata mitte negatiivset tingimust. Mõne samaväärse funktsiooni maksimeerimine, et minimeerida sama funktsiooni vastupidise märgiga ja vastupidi.

Lineaarse programmeerimise ülesande reegel kanoonilise välimuse jaoks on järgmine:

kui allikate ülesanne teil on vaja määrata maksimaalne lineaarne funktsioon, siis peaks muutma märk ja otsima minimaalset selle funktsiooni;

kui piirangutes on õige osa negatiivne, siis see piirab seda piiri -1;

kui piirangute seas on ebavõrdsus, siis lisatakse need täiendavad mitte-negatiivsed muutujad võrdõiguslikkusena;

kui mõni muutuja x. j. Märgi piiranguid ei asendata (sihtfunktsioonis ja kõikides piirangutes) kahe uue mitte-negatiivse muutuja vahe: x. 3 \u003d X. 3 + - X. 3 - kus x. 3 + , X. 3 - ≥ 0 .

Näide 1.. Lineaarse programmeerimisprobleemi kanoonilise vormi toomine:

min l \u003d 2x 1 + X. 2 - X. 3 ; 2x. 2 - X. 3 ≤ 5; X. 1 + X. 2 - X. 3 ≥ -1; 2x. 1 - X. 2 ≤ -3; X. 1 ≤ 0; X. 2 ≥ 0; X. 3 ≥ 0.

Tutvustame iga piirangute süsteemi võrrandile nivelleerimismuutujate x. 4 , X. 5 , X. 6 . Süsteem registreeritakse võrdsete kujul ja muutujate piirvasüsteemi esimeses ja kolmandates võrranditel x. 4 , X. 6 sisestatud vasakule osale "+" märk ja teise võrrandi muutuja x. 5 Sisestatud märk "-".

2x. 2 - X. 3 + X. 4 \u003d 5; X. 1 + X. 2 - X. 3 - X. 5 \u003d -1; 2x. 1 - X. 2 + X. 6 \u003d -3; X. 4 ≥ 0; X. 5 ≥ 0; X. 6 ≥ 0.

Tasuta liikmed Canonical vormis peaks olema positiivne, sest viimased kaks võrrandit korrutatakse -1:

2x. 2 - X. 3 + X. 4 \u003d 5; -X. 1 - X. 2 + X. 3 + X. 5 \u003d 1; -2x 1 + X. 2 - X. 6 = 3.

Simplexi meetod lineaarsete programmeerimisülesannete lahendamisel.

Simplexi meetodi algoritm leiab optimaalse lahenduse, arvestades piiratud arvu lubatud lahendusi. Simplexi meetodi algoritm algab alati mõne kehtiva aluse lahendusega ja seejärel püüab leida teise kehtiva aluse lahenduse, "parandades" sihtfunktsiooni väärtust. See on võimalik ainult siis, kui nulli (mitte-peekon) muutuja suurenemine toob kaasa sihtfunktsiooni väärtuse paranemisele. Kuid selleks, et mittepommide muutuja muutub positiivseks, tuleks üks praegustest põhilistest muutujatest nullida, st. Tõlgi magid. On vaja, et uus lahendus sisaldab täpselt m. Põhilised muutujad. Simplexi meetodi terminoloogia kohaselt nimetatakse valitud nullmuutujat sisenes (Põhjas) ja eemaldatud põhiline muutuja - Üüritanud (põhjal).

Kaks sisestatud valimise ja väljajätvate muutujate valimise reeglit optimaalsuse seisund ja lubatavuse seisund . Me sõnastame need reeglid, samuti kaalume Simplexi meetodi rakendamisel tehtud toimingute järjestust.

Optimaalsuse seisund. Lisatud muutuja maksimeerimise probleem (minimeerimine) on tasakaalustamata muutuja, millel on suurim negatiivne (positiivne) koefitsient sihtmärk-Kogu. Kui see on sihtmärk- On mitmeid selliseid koefitsiente, muutuja valitud muutuja valik tehakse meelevaldselt. Optimaalne lahendus saavutatakse siis sihtmärk- Kõik koefitsiendid mitte-kuritarvitamise muutujatega ei ole negatiivne (mitte-positiivne).

Vastuvõetavuse tingimus. Nagu maksimeerimisprobleemil ja minimeerimisülesandel ja minimeerimisülesandel, valitakse aluse muutuja välistamiseks, mille puhul juhtiva veeru positiivse koefitsiendi piirangute parempoolse osa väärtuse suhe on minimaalne. Kui sellise vara puhul on mitmeid põhilisi muutujaid, teostatakse välistatud muutuja valik suvaliselt.

Andke meile algoritmi lahendada lineaarse programmeerimisülesande, et leida maksimaalne lihtsate simplex tabelite abil.

F \u003d C1 x 1 + C2 x 2 + ... + n x n maxiga

x 1 0, x 2 0, ..., x n 0.

1. samm. Tutvustame täiendavaid muutujaid ja kirjutada saadud süsteemi võrrandid ja lineaarne funktsioon laiendatud süsteemi.

F-C 1 x 1-C2 x 2 - ... -c n x n \u003d 0 \u003d c p.

2. samm. Me koostame esialgse Simplex tabeli.

Muutujad	Põhi- ja lisaainete muutujad	tasuta liikmed (otsus)	Hinnanguline suhtumine
Muutujad		tasuta liikmed (otsus)	Hinnanguline suhtumine

3. samm. Me kontrollime optimaalsuse kriteeriumi täitmist - negatiivsete koefitsientide viimases reas. Kui sellist ei ole, siis lahendus on optimaalne ja f * \u003d CO, põhilised muutujad on võrdsed vastavate koefitsientidega B J, mitte-neurovabad muutujad on , st x * \u003d (b 1, b 2, ..., BM, 0, ..., 0).

4. samm. Kui optimaalsuse kriteerium ei ole täidetud, määratakse viimase (hinnangulise) stringi kõrgeim negatiivne koefitsient lubatud veerus s.

Resolutsioon-stringi määramiseks arvutage hinnanguline suhe ja täitke tabeli viimane veerg.

I-Th rida hinnanguline suhe

 Kui b i ja a on erinevad märgid;

, kui b i \u003d 0 ja a on<0;

, kui a on \u003d 0;

0, kui b i \u003d 0 ja a on\u003e 0;

Hindamise suhe veerus leiame minimaalse minimeelemendi mis määrab g stringi eraldusvõime.

Kui minimaalne ei ole, ei ole ülesanne lõplik optimaalne I ja on raske.

Resolutsioonide ristumiskohas on ridade ja veerude ristumiskohas GS-i lubatud element.

5. samm. Ehitada järgmine tabel. Selle jaoks

Mine kolmanda sammu juurde.

M-meetod on mõnikord ZLP lahendamisel koefitsientide maatriksis tundmatute limiidisüsteemides ei ole ühtegi veergu, millest saab teha ühe maatriksi, st Põhimuutujate valimise probleem tekib või esialgne lahendus on kehtetu. Sellistel juhtudel kasutage tehnilise aluse meetod (M - meetod).Kõigis piirangutes, kus puuduvad põhilised muutujad, sisestatud kunstlikud muutujad. Sihtfunktsioonis on kunstlikud muutujad kasutusele koefitsiendiga (- m) maksimaalsete ülesannete ja koefitsiendiga (+ m) Min ülesannete puhul, kus m on piisavalt suur positiivne number. Seejärel lahendatakse laiendatud ülesanne Simplexi meetodi reeglite kohaselt. Kui kõik kunstlikud muutujad on võrdsed nulliga, s.o Nad kustutatakse põhjal, kas esialgse ülesande optimaalne lahendus saadakse või esialgne ülesanne lahendatakse edasi ja selle optimaalne lahendus asub või selle lahustatavus on asutatud. Kui vähemalt üks kunstliku muutuja on erinev nullist, siis esialgse ülesandel ei ole lahendust

Universaalset meetodit LP probleemide lahendamisel nimetatakse Simplexi meetodiks. Selle meetodi kasutamine ja selle kõige tavalisem muutmine on kahefaasilise simplex meetod.

Graafilise meetodi lahendamise probleemide lahendamisel LP, me tegelikult hulgast tippu kuuluvate tippude piiri kehtestatud lahendusi ebavõrdsuse süsteemi valis sellise tipu, milles väärtus sihtfunktsiooni saavutas maksimaalse (minimaalse). Kahe muutuja puhul on see meetod täiesti visuaalne ja võimaldab teil probleemi lahenduse kiiresti leida.

Kui ülesandeks on kolm ja rohkem muutujaid ja reaalsed majanduslikud ülesanded just sellise olukorraga, on raske ette kujutada piirangute lahenduste visuaalset valdkonda. Sellised ülesanded lahendatakse simplex meetod või järjestikuste paranduste meetodit. Meetodi idee on lihtne ja on järgmine.

Teatava reegli kohaselt asub esialgne võrdlusplaan (mõned tipud piirangud). Kontrollitud, kas plaan on optimaalne. Kui jah, siis ülesanne lahendatakse. Kui ei, siis minge teisele paremale plaanile - teisele tipule. Selle plaani sihtfunktsiooni väärtus (selles ülaosas) on teadlikult parem kui eelmisel. Ülemineku algoritm viiakse läbi mõned arvutustapi, mis on mugav salvestada tabelite kujul simplex tabelid . Kuna tipud on piiratud arv, siis lõpliku arvu samme tuleme optimaalsele lahendusele.

Kaaluge simplexi meetodit plaani koostamise ülesannete konkreetsel näitel.

Jällegi märgime, et Simplex-meetod on kohaldatav LP kanooniliste probleemide lahendamisel, mis antakse erivormile, mis on aluseks, positiivsed õiged osad ja sihtfunktsioon, mis on väljendatud mitte-peekoni muutujate kaudu. Kui ülesanne ei ole erilist vormi näidanud, on vaja täiendavaid samme, mida me räägime hiljem.

Kaaluge tootmiskava ülesandeks, mudeli eelregistreerimise ja selle juhtimise aluseks.

Ülesanne.

Toodete valmistamiseks AGA ja Sisse Ladu võib vabastada tooraineid mitte rohkem kui 80 ühikut. Ja toote valmistamisel AGA Kaks ühikut tarbitakse ja tooted Sisse - üks tooraineühik. Tootmise planeerimiseks on vaja planeerida nii, et suurim kasum oleks tooted AGA See on kohustatud tegema rohkem kui 50 tk. Ja tooted Sisse - Mitte rohkem kui 40 tk. Ja ühe toote rakendamise kasum AGA - 5 rubla. Ja alates Sisse - 3 rubla.

Me ehitame matemaatilise mudeli, mis näitab h. 1 toodete arv ja selle osas h. 2 - toodete arv Sisse. Seejärel näeb välja selline restriktsioonisüsteem:

x 1 ≤50.
x 2 ≤40.
2x 1 + x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 + 3x 2 → max

Me anname ülesande kanoonilisele vormile, sisestades täiendavaid muutujaid:

x 1 + x 3 \u003d 50
x 2 + x 4 \u003d 40
2x 1 + x 2 + x 5 \u003d 80
x 1 ≥0, x 2 ≥0
5x 1 + 3x 2 → max
-F \u003d -5x 1 - 3x 2 → min.

Sellel ülesandel on eriline välimus (põhjal, õiged osad on mitte-negatiivsed). Seda saab lahendada Simplex meetodil.

I. etapp. Salvestage ülesanne Simplex tabelis. Probleemi süsteemi piirangute (3.10) ja Simplex tabeli vahel on mitme kirjavahetus. Liinid tabelis nii palju võrdsed süsteemi piirangute ja veergude - nii palju kui vaba muutujad. Põhilised muutujad täidavad esimese veeru, tasuta - tabeli ülemine rida. Alamjoont nimetatakse indeksiks, koefitsiendid salvestatakse sihtfunktsioonis muutujatega. Alumises paremas nurgas on see algselt kirjutatud 0, kui funktsiooni ei ole vaba liiget; Kui on olemas, kirjutage see vastupidisele märgile. Selles kohas (alumises paremas nurgas) on sihtfunktsiooni väärtus, mis ühest tabelist liikumisel tuleks mooduli abil suurendada. Niisiis, meie piirangute süsteem vastab tabelile 3.4 ja saate jätkata lahenduse II etappi.

Tabel 3.4.

alus			vaba

II. etapp. Optimaalsuse toetusplaani kontrollimine.

See tabel 3.4 vastab järgmisele võrdlusplaanile:

(h. 1 , h. 2 , h. 3 , h. 4 , h. 5) = (0, 0, 50, 40, 80).

Vaba muutujad h. 1 , h. 2 on võrdsed 0-ga; h. 1 = 0, h. 2 \u003d 0. ja põhilised muutujad h. 3 , h. 4 , h. 5 Võtke väärtused h. 3 = 50, h. 4 = 40, h. 5 \u003d 80 - vaba liikmete veerus. Sihtfunktsiooni väärtus:

-F. = - 5h. 1 - 3h. 2 \u003d -5 · 0 - 3 · 0 \u003d 0.

Meie ülesanne on kontrollida, kas see võrdlusplaan on optimaalne. Selleks vaadake indeksi string - sihtfunktsiooni rida F..

Erinevad olukorrad on võimalikud.

1. India F.- Netos ei ole negatiivseid elemente. Niisiis on plaan optimaalne, probleemile on võimalik kirjutada lahendus. Sihtfunktsioon saavutas oma optimaalse väärtuse, mis on võrdne paremas nurgas, mis on võetud vastupidise märgiga. Mine IV etappi.

2. indeksi liinil on vähemalt üks negatiivne element, milles ei ole positiivset veergu. Siis järeldame, et sihtfunktsioon F.→ ∞ piiramatu väheneb.

3. Indeksiliinis on veerus negatiivne element, mille puhul on vähemalt üks positiivne. Siis mine järgmise III etapi juurde. Tabeli tagasilükkamine referentskava parandamisel.

III etapp. Võrdlusplaani parandamine.

Negatiivsete elementide indeksist F.- valime mooduli suurima mooduli, helistagem veergu, mis vastab sellele on lubada ja märkida. "

Stringi eraldusvõime valimiseks on vaja arvutada vaba liikmete veeru elementide suhe ainultet positiivne Resolutsiooni kolonni elemendid. Valige saadud suhted on minimaalne. Minimaalselt saavutatav vastav element nimetatakse lubavaks. Me jaotame selle ruuduga.

Meie näites on element 2 lubav. Sellele elemendile vastavat string nimetatakse ka eraldusvõimeks (tabel 3.5).

Tabel 3.5

Valides Lubamisobjekti, teeme nimekirja tabeli järgi vastavalt reeglitele:

1. Uues tabelis sama suurusega nagu varasemad muutujad lubatud string ja veerg varieeruvad kohtades, mis vastab üleminekule uuele alusele. Meie näites: h. 1 siseneb selle asemel h. 5, mis väljub baasist ja nüüd tasuta (tabel 3.6).

Tabel 3.6.

2. Resolutsiooni elemendi 2 asemel kirjutage vastupidine number ½.

3. Lennukringi elemendid on jagatud lubatud elemendina.

4. Resolutsiooni kolonni elemendid jagavad lubamispunkti ja kirjutage vastupidise märgiga.

5. Täitmiseks ülejäänud elemendid tabelis 3.6, me ümberarvutatud vastavalt ristkülik reegel. Olgume, et me tahame arvutada elemendi seisab asemel 50.

Me ühendame selle elemendi vaimselt resolutsiooniga, leiame tükk, me lahutame selle elementide toote, mis on teise saadud ristküliku diagonaal. Erinevus jaguneb lubamismärgile.

Niisiis ,. Kirjutame 10 kohale, kus oli 50. Samamoodi:
, , , .

Tabel 3.7.

Meil on uus tabel 3.7, põhilised muutujad on nüüd muutujad (x 3, x 4, x 1). Sihtfunktsiooni väärtus on muutunud võrdseks -200-st, st vähenenud. Selle põhilise lahenduse kontrollimiseks optimaalsusele peate minema uuesti 2. etappi. Protsess on ilmselgelt piiratud, peatuse kriteerium on etapi lõigete 1 ja 2.

Me lahendame probleemi lõpuni. Selleks kontrollige indeksi stringit ja vaadake negatiivset elementi -1 IT-s, me nimetame selle jaoks sobivale veerule ja vastavalt III etapi andmetele ümberakesta tabelit. Suhete koostamisega ja nende hulgas minimaalse \u003d 40 valimine, määratakse kindlaks, millist elementi 1. Nüüd ümberakestame reeglite kohaselt 2-5.

Tabel 3.8.

Pärast tabeli ümber arvutamist oleme veendunud, et indeksi liinil ei ole negatiivseid elemente, seetõttu lahendatakse ülesanne, põhiplaan on optimaalne.

IVetapp. Kõrvaldamise optimaalne lahendus.

Kui Simplex meetod peatati vastavalt 1. etapi andmetele 1, siis probleemi lahendus on kirjutatud järgmiselt. Põhilised muutujad võtavad vastavalt vaba liikmete veergu väärtusi. Meie näites h. 3 = 30, h. 2 = 40, h. 1 \u003d 20. Vaba muutujad on 0, h. 5 = 0, h. 4 \u003d 0. Sihtfunktsioon võtab vastupidise märgiga tasuta liikmete veeru viimase elemendi väärtuse: - F. = -220 → F.\u003d 220, meie näites uuriti funktsiooni min ja esialgu F. → MAX, nii et tegelikult on kaubamärk kaks korda muutunud. Niisiis, h.* = (20, 40, 30, 0, 0), F.* \u003d 220. Vastus ülesandele:

On vaja lisada 20 tüüpi tooteliiki AGA, 40 B-tüüpi tooteid ja kasum on maksimaalne ja on võrdne 220 rublaga.

Selle osa lõpus esitame simplexi meetodi algoritmi plokkskeemi, mis kordab täpselt samme, kuid võib-olla mõnede lugejate jaoks on mugavamad kasutamiseks mugavamad, kuna nooled näitavad meetmete selget orienteeritust.

Volsikardal olevate ristkülikute ülaltoodud viited näitavad, et vastav ümberkujunduste rühm on seotud selle etapi või alamklausliga. Esialgse võrdlusplaani leidmise reegel sõnastatakse punktis 3.7.

Näide. Lahenda järgmine ülesanne LP kanoonilise vormi simplex meetod.
f (x) \u003d x 1 + 9x 2 + 5x 3 + 3x 4 + 4x 5 + 14x 6 → min
x 1 + x 4 \u003d 20
x 2 + x 5 \u003d 50
x 3 + x 6 \u003d 30
x 4 + x 5 + x 6 \u003d 60
x i ≥ 0, i \u003d 1, ..., 6
On öeldud, et LP ülesanne on kanooniline vorm, kui kõik piirangud (välja arvatud mittetagata muutuvatele muutujatele) on võrdsete võimaluste kujul ja kõik vabad liikmed ei ole negatiivsed. Nii et meil on kanoonilises vormis ülesanne.
Simplexi meetodi idee on järgmine. Kõigepealt peate leidma PolyHedroni lubatud lahenduste mõned (esialgse) tipu (esialgne lubatav alus). Siis peate selle lahenduse optimaalsuse jaoks kontrollima. Kui see on optimaalne, siis leitakse lahus; Kui ei, siis mine teise ülaosas polühedroni ja kontrollige uuesti optimaalsuse. Polühedroni tippude jäsemete tõttu (LP-i ülesande piirangute jäsemejäsemete tagajärjed) lõpliku arvu "sammude" jaoks leiame soovitud minimaalse või maksimaalse määramise punkti. Tuleb märkida, et ühe tipu teise liikumisel väheneb sihtfunktsiooni väärtus (minimaalse probleemiga) või suureneb (maksimaalse ülesannete täitmisel).
Seega põhineb Simplexi meetodi idee LP ülesande kolmel omadustel.
Otsus. Et leida esialgne lubatud põhiline lahendus, st Põhiliste muutujate määramiseks tuleb süsteem (5.6) viia "diagonaal" meeles. Gauss'i meetodi rakendamine (teadmata tundmatu väljaarvamise meetod), saame alates (5.6):
x 2 + x 1 + x 3 \u003d 40
x 4 + x 1 \u003d 20
x 5 -x 1 -x 3 \u003d 10
x 6 + x 3 \u003d 30
Järelikult on põhilised muutujad x 2, x 4, x 5, x 6,nad lisavad väärtusi, mis on võrdsed vastavate liinide tasuta liikmetega: x 2 \u003d 40, x 4 \u003d 20, x 5 \u003d 10, x 6 \u003d 30,. Muutujad x 1 ja x 3. on magid: x 1 \u003d 0, x 3 \u003d 0.
Ehita esialgne lubatav lahendus
x 0 \u003d (0,40,0,20,10,30) (5.9)
Leitud lahenduse optimaalsuse kontrollimiseks x 0. On vaja välja jätta põhifunktsioonist põhifunktsioonist (kasutades süsteemi (5.8)) ja ehitada spetsiaalne simplex tabel.
Pärast muutujate väljajätmist on sihtfunktsioon mugav kirjutada kujul:
f (x) \u003d -7x 1 - 14x 3 +880 (5.10)
Nüüd koos (5.8) - (5.10) Teeme esialgse simplex tabeli:

Koefitsiendid salvestatakse nulljoonega, mille eesmärk on vastavate muutujate vastupidine märk sihtfunktsioonis. Optimaalsuse kriteerium (minimaalse otsinguülesande jaoks): lubatud baaslahendus ( x 0.) Optimaalselt, kui nulljoonel ei ole ühtegi rangelt positiivset numbrit (sihtfunktsiooni väärtuse arvestamine (880)). Seda reeglit kohaldatakse järgmiste iteratsioonide suhtes (tabelid). Null rida elemente nimetatakse veeru hinnanguteks.
Seega ei ole esialgne lubatud põhiline lahendus (5.9) optimaalne: 7>0, 14>0 .
Null kolonnis salvestatakse põhiliste muutujate väärtused. Need peavad tingimata olema negatiivsed (vt võrrandit (5.7)). Alates esimesest neljandale reale on kirjutatud süsteemi muutujate koefitsiendid (5.8).
Kui x 0. Mitte optimaalselt, siis peate minema teisele tipule polühedroni lubatud lahendusi (ehitada uus D. B.R.). Selle tegemiseks leidke juhtiv element ja läbi konkreetse konversiooni (simplex transformatsioon).
Esiteks leiame tabeli juhtiv element, mis on juhtiva veeru ristumiskohas (veerg suurima positiivse hinnanguga) ja vastuvõtva stringi (stringidega, mis vastavad nullkolonali elementide minimaalsele suhtele vastavatele elementidele (rangelt) positiivne) juhtiv kolonn).
Tabelis 1 on juhtiv kolonn kolonn ja juhtiv joon on neljas rida (Min (40 / 1.30 / 1) \u003d 30/1) Märgistatud noolega ja juhtiv element on ring. Plii element näitab, et põhiline muutuja x 6. tuleb asendada mitte-kuritarvitamisega x 3.. Siis on uued põhilised muutujad x 2, x 3, x 4, x 5,ja mitte-lahtiühendamine - x 1, x 6,. See tähendab üleminekut polühedroni lubatud lahenduste uuele tippudele. Uue lubatud põhilise lahenduse koordinaatide leidmiseks x 00. Te peate ehitama uue simplex tabeli ja teostama elementaarseid muutusi selles:
aga) Kõik vastuvõtva stringi elemendid on jagatud juhtivaks elemendiks selle juhtiva elemendi muutmisel 1 (arvutuse lihtsustamiseks);
b) Draivielemendi kasutamine (1), kõik juhtiva veeru elemendid muutuvad nulliteks (sarnased teadmata) väljajätmise meetodiga);
Selle tulemusena saadi nullkolonnis uute põhiliste muutujate väärtused. x 2, x 3, x 4, x 5, (Vt tabel 2) - uue tipu põhikomponendid x 00. (Nebase komponendid x 1 \u003d 0, x 6 \u003d 0,).

Nagu tabel 2 näitab, uus baaslahendus x 00 \u003d (0,10,30,20,0,0) Optimaalselt (nulljoonel on mitte-negatiivne hinnang 7). Seega, juhtiv element 1 (vt tabel 2) ehitame uue simplex tabeli, st Ehita uus lubatud lahendus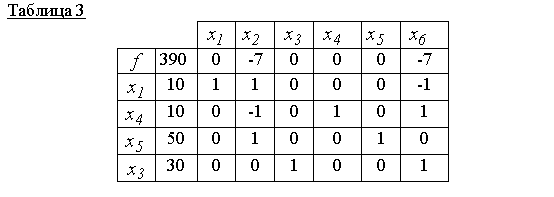

Tabel 3 vastab lubatud põhilahusele x 000 \u003d (10,0,30,10,50,0) Ja see on optimaalne, sest Nulljoonel puuduvad positiivsed hinnangud. seetõttu f (x 000) \u003d 390 Sihtfunktsiooni minimaalne väärtus.
Vastus: x 000 \u003d (10, 0, 30, 10, 50, 0) - minimaalne punkt, f (x 000) \u003d 390.

Tingimuslikult tavaline lineaarne programmeerimisülesanne

Te peate täitma järgmised ülesanded kindlaksmääratud järjekorras.

Leia parim plaan otsese ülesande jaoks:
a) graafiline meetod;
b) Simplex-meetod (allika võrdlusplaani loomiseks on soovitatav kasutada kunstlikku meetodit).
Ehita kahekordne ülesanne.
Leia parim omadus kahekordne ülesanne graafilisest lahendusest otseselt kasutades täiendava jama tingimusi.
Leia optimaalne plaan kahekordse probleemi esimesel duality teoreemil, kasutades otsese ülesande lahendamisel saadud lõplikku simplex tabeli (vt lõik 1b). Kontrollige heakskiidu "väärtused sihtfunktsioonide paari kahekordsete ülesannete oma optimaalsete lahenduste kattumine."
Dual ülesanne on lahendada simpleks-meetod, seejärel kasutades lõplik simplex tabel dual ülesande leida optimaalne plaan otsese ülesande jaoks esimese duality teoreemi otsese ülesande jaoks. Võrdle tulemust tulemusega, mis saadi graafilise meetodi abil (vt lõik 1a).
Leia optimaalne täisarvlahendus:
a) graafiline meetod;
b) homori meetod.
Võrdle täisarvu funktsioonide väärtusi ja mitte järgnevaid lahendusi

Küsimused enesekontrolli küsimused

Kuidas Simplex tabel ehitatakse?
Kuidas tabeli baasmuutus peegeldab?
Sõna sümbolimeetodi peatamise kriteerium.
Kuidas korraldada tabeli muutmist?
Millisest joonist on tabeli läbimine mugav?

Appleti lahendamiseks arvutisse peate tegema järgmise - klõpsake nuppu Start\u003e Control Panel\u003e Programs\u003e Java. Java juhtpaneeli aknas valige vahekaart Turvalisus (Turvalisus) Vajutage nuppu Muuda nimekirja nuppu, lisa nupule ja sisestage sellele lehele tee brauseri aadressirealt tasuta väljale. Järgmisena vajutage nuppu OK nupud, seejärel taaskäivitage arvuti.

Appleti käivitamiseks klõpsa nupule "Simplex". Kui nupp "Simplex" ei ole selle stringi kohal nähtav, ei ole Java arvutisse installitud.

Pärast nupu "Simplex" vajutamist kuvatakse esimene aken muutujate arvu sisestamiseks ja ülesande piirangute arv Simplexi meetodile.

Pärast nupule "OK" klõpsamist kuvatakse aken Simplexi ülesannete järelejäänud ülesandeandmete sisestamiseks: kuvarežiim (kümnendad fraktsioonid või tavalised), minimaalse kriteeriumi tüübist või maksimaalse probleemi tüübist, sisestab sihtfunktsiooni koefitsiendid ja piirvesüsteemi koefitsiendid tähistega "≤", "≥" või "\u003d", liigi X I ≥ 0 piirangute piirangud ei ole vaja sisestada, \\ t Neid võetakse arvesse nende algoritmis.

Pärast nupule "Lahenda" klõpsamist kuvatakse probleemi lahendamise tulemustega aken . Aken koosneb kahest osast, tekstivälja on ülaosas, mis sisaldab esialgse ülesande esitamise kirjeldust kanoonilisele vormile, mida kasutatakse esimese simplex tabeli koostamiseks. Paneelides asuva akna allosas on iga iteratsiooni simplex tabelid, millel on väike tekstivälja allosas, mis näitab, millist veergu, mis võimaldab treeningprogrammi tegemist ja muud teavet. Vahekaardil tekstivälja optimaalse (viimase) tabeliga antakse saadud optimaalne lahuse lahus.

Valitud vead ja kommentaarid apleti kohta saadetakse [E-posti kaitstud] Või helistage 8 962 700 77 06, mille jaoks me oleme teile väga tänulikud.

M-meetodi programm

Transpordiprobleemi lahendamise programm

Siin on käsitsi (mitte aplet) kahe ülesande lahendus Simplexi meetodiga (sarnane apleti lahendus) üksikasjalike selgitustega, et mõista probleemi lahendamise algoritmi. Esimene ülesanne sisaldab ainult ebavõrdsuse tähiseid ainult "≤" (esialgse alusega ülesanne), teine \u200b\u200bvõib sisaldada märke "≥", "≤" või "\u003d" (kunstliku alusega ülesanne), need lahendatakse erinevalt.

Simplex-meetod, ülesande lahendamine esialgse alusega

1)Simplex meetodesialgse aluse ülesande täitmiseks (kõik ebavõrdsuse tunnused "≤").

Me kirjutame ülesande B. kanooniline Vorm, s.o. Ebavõrdsuse piirangud kirjutab ümber võrdsuste vormis tasakaal Muutujad:

See süsteem on süsteemi alusega (alus S 1, S 2, S 3, igaüks neist siseneb ainult ühe võrrandi süsteemi koefitsiendiga 1), x 1 ja x 2 - vaba muutujaid. Ülesanded, kui lahendamisel Simplex-meetodi rakendatakse, peab olema järgmised kaks omadust:
- piirangute süsteem peaks olema võrdsete süsteemide süsteem;
- Süsteemi kõigi võrrandite toetatavad tingimused peavad olema mitte-negatiivsed.

Saadud süsteem on süsteemi aluse ja selle vaba liikmed on mittegatiivsed, nii et saate rakendada Simplex meetodit. Tehke esimene simplex tabel (iteratsioon 0), st Sobivate muutujatega sihtfunktsioonide koefitsientide ja võrrandite süsteemi tabel. Siin tähendab "BP" põhiliste muutujate veeru, "lahendus" - süsteemi võrrandite parema osa veerus. Otsus ei ole optimaalne, sest Z-liinis on negatiivsed koefitsiendid.

iteratsioon 0.

Bp	Otsus	Suhtumine

Lahenduse parandamiseks pöördume järgmise iteratsiooni poole, saame järgmise Simplex tabeli. Selleks peate valima lubav veerg. Muutuja, mis sisestab järgmise iteratsiooni aluse. See valib suurim moodul negatiivse koefitsiendi jaoks Z-reas (maksimaalsest probleemsest) - esialgses iteratsioonis See veerg x 2 (koefitsient -6).

Seejärel valitud eraldusvõimega string. Muutuja, mis on järgmisel iteratsiooni alusest väljas. See valitakse veeru väikseim suhtumine resolutsioonikolonni vastavatele positiivsele elementidele (kolonn "suhe") - esialgses iteratsioonis on see string S 3 (koefitsient 20).

Elementide lubamine Asub resolutsioonikolonni ristumiskohas ja resolutsioonis eraldatakse selle rakk värviga, see on 1. Seega järgmisel iteratsioonis asendatakse varieeruv X2 põhjal S 3. Pange tähele, et Z-rida suhtumine ei otsi, seal on kriips "-". Juhul kui on olemas sama minimaalne suhe, siis ükskõik milline neist on valitud. Kui kõik koefitsiendid on eraldusvõime veerus väiksemad või võrdsed, on probleemide lahendamine lõpmatu.

4) stringi S 2 tabeli "iteratsiooni arvutamine 1". Kohas 3 S 2 rida "iteratsiooni 0" tabelis peaks olema 0 "iteratsiooni 1" tabelis. Selleks, kõik elemendid string x 2 tabel "iteratsioon 1" 0 1 0 0 1 20 korrutada -3, saame 0 -3 0-3 -60 ja panna see string S 2-ga Tabel "Iteratsiooni 0" 1 3 0 1 0 72, saame stringi 1 0 0 1 -3 12. Veerus X2 soovitud 0 saadakse. Veerg X 2 "iteratsiooni 1" tabelis muutus üheks See sisaldab ühte 1 ja ülejäänud 0.

Ridade "iteratsiooni 1" tabel saadakse vastavalt järgmisele reeglile:

Uus rida \u003d vana string - (vana liini lubava veeru koefitsient) * (uus lubav string).

Näiteks Z-jaoks on meil:

Vana Z-rida (-4 -6 0 0 0 0)
- (- 6) * Uus võimaldab string - (0-6 0 0 -6 -120)
\u003d Uus Z-rida(-4 0 0 0 6 120) .

Järgmiste tabelite puhul tehakse tabeli elementide ümberarvutamine sarnaselt, nii et me jätkasime seda.

iteratsioon 1.

						Otsus	Suhtumine

Iteratsioon 2.

						Otsus	Suhtumine

Resolutsioonis kolonn S 3, stringi S 1, S 1 lahustub aluse, S 3 siseneb aluse.

Iteratsioon 3.

						Otsus	Suhtumine

Z-reas kõik koefitsiendid on mitte-negatiivsed seetõttu optimaalne lahus x 1 \u003d 24, x 2 \u003d 16, z max \u003d 192 saadi.

Simplex-meetod, mis lahendab ülesanne tehispõhiselt

2) Ma lahendan ülesande kunstliku alusega (vähemalt üks ebavõrdsuse märkide märk "≥" või "\u003d").

Kirjutame ülesande kanoonilises vormis (võrrandite süsteem, mis nõuab simplexi meetodit), selle eest tutvustame kaks muutujat x 3 ≥ 0 ja x 4 ≥ 0

Piirisüsteem pakub ainult ühte lubatud põhilist muutust X 4, vaid siseneb ainult ühe võrrandi kolmas koos koefitsiendiga 1, seetõttu lisage esimeses ja teises võrrandis kunstlikke muutujaid R1 ≥ 0 ja R2 ≥ 0 Rakenda Symplex-meetodi süsteem Piirangute võrrandid peavad olema süsteemi alusega, st Igas võrrandis peab olema muutuja koefitsiendiga 1, mis kuulub ainult ühe süsteemi võrrandile, meie puhul on see R1, R2 ja X4. Saadud, nn m-ülesanne:

See süsteem on süsteemi alusega süsteem, kus R1, R2 ja X4 on põhilised muutujad ja X1, X2 ja X 3 vaba muutujad, kõigi võrrandite liikmed ei ole negatiivsed. Järelikult saate probleemi lahendada, saate rakendada Simplexi meetodit. Me kirjutame esialgse simplex tabeli:

iteratsioon 0.

	Otsus	Suhtumine
-16

Kunstliku aluse ülesannete jaoks lisati tabelile string "Hindamine". See on saadud vastavate ridade koefitsientide summeerimisega kunstlike muutujatega (R) vastupidise märgiga. See on tabelis, kuni vähemalt üks kunstlikest muutujatest on aluses. Kõige mooduli jaoks määratakse stringi "reiting" negatiivne reiting, mis võimaldab tabelis lauale lubamist. Kui string "hindamine" vabastatakse tabelist (baasil ei ole kunstlikke muutujaid) Lubav veerg määrab Z-Rida, nagu ülesandel esialgse alusega. Selles tabelis on resolutsioon X2 veerg, see valitakse kõrgeima negatiivse hinnangu (-7) mooduli järgi.Resolutsioonjoon R2 valitakse väikseima suhtega "lahuse" kolonni väiksema suhtega eraldusvõime veeru vastavatele positiivsele elementidele, nagu probleem ilma kunstlike muutujateta. See tähendab, et järgmistes iteratsioonis lülitub vaba muutuja X 2 põhilisele ja varieeruvale R2 põhilisele - vabale. Kirjutame järgmise Simplex tabeli:

Resolutsioonis X 1, R1, R1 lahutamine, R1 jätab aluse, X 1 siseneb aluse. Pärast seda ei ole aluse kunstlikke muutujaid, mistõttu ei ole järgnevas tabelis ridade hindamist "hindamist":

iteratsioon 2.

							Otsus	Suhtumine

Seejärel valitakse veerg Z-rida poolt. Z-reas kõik koefitsiendid ei ole mitte-negatiivsed kui koefitsient kunstliku varieeruva R1, mis ei mõjuta optimaalsust, kui kunstlikud muutujad lahkus alusest. Seetõttu saadi optimaalne lahus x 1 \u003d 6/5; x 2 \u003d 3/5; Z MAX \u003d 72/5.

Simplexi meetodi erijuhtumid

1) kui sirge (kui kahemõõtmeline lineaarne programmeerimisprobleem on ja üldise juhtumi hüperplaneris), esindades sihtfunktsiooni paralleelselt sirge (hüperplane), mis vastab ühele ebavõrdsusele piirangutega (mis optimaalses punktis on Tehtud täpse võrdõiguslikkusena) Sihtfunktsioon võtab ühe ja ka optimaalse väärtuse teatud piirkonna piiri piirkonna piirkonna piirkonnas lubatud lahendusi. Neid lahendusi kutsutakse alternatiivsed optimaalsed lahendused. Alternatiivsete lahenduste olemasolu saab määrata optimaalse simplex tabeliga. Kui optimaalse tabeli Z-rida on null-koefitsiendid mittesiduvate muutujate, on alternatiivsed lahendused.

2) Kui simplex tabeli kolonnis on kõik koefitsiendid väiksemad või võrdsed nulliga, siis ei saa valida stringi eraldusvõimet, antud juhul on lahus piiramatu.

3) Kui lineaarse programmeerimisprobleemi piirangud on puudulikud (s.o neid ei saa samaaegselt läbi viia), siis ülesandel ei ole kehtivaid lahendusi. Selline olukord ei pruugi esineda, kui kõik piirangute süsteemi ebavõrdsusel on tüüp "≤" mittegatiivsete õigete osadega, sest Sellisel juhul võivad täiendavad muutujad teha lubatud lahenduse. Muude piirangute puhul kasutatakse kunstlikke muutujaid. Kui ülesandel on lahendus, siis ei ole baasil (r I) alust kunstlikke muutujaid. Kui nad on olemas, ei ole ülesanne lahendusi.