Proportional segments in a right triangle. Lesson "proportional segments in a right triangle" How to find proportional segments in a right triangle
Lesson 40 C. b. a. h. C. bc. H. ac. A. V. The height of a right triangle, drawn from the vertex of a right angle, divides the triangle into 2 similar right triangles, each of which is similar to a given triangle. Sign of similarity of right triangles. Two right triangles are similar if they each have the same acute angle. The segment XY is called the mean proportional (geometric mean) for the segments AB and CD if Property 1. The height of a right triangle drawn from the vertex of the right angle is the mean proportional between the projections of the legs onto the hypotenuse. Property 2. The leg of a right triangle is the mean proportional between the hypotenuse and the projection of this leg onto the hypotenuse.
Slide 28 from the presentation "Geometry "Similar Triangles"". The size of the archive with the presentation is 232 KB.Geometry Grade 8
summary of other presentations"Solution of problems on the Pythagorean theorem" - Triangle ABC isosceles. Practical application of the Pythagorean theorem. ABCD is a quadrilateral. Square area. Find sun. Proof. Bases of an isosceles trapezoid. Consider the Pythagorean theorem. Area of a quadrilateral. Rectangular Triangles. Pythagorean theorem. The square of the hypotenuse is equal to the sum of the squares of the legs.
"Finding the area of a parallelogram" - Foundation. Height. Determining the height of a parallelogram. Signs of equality of right triangles. The area of a parallelogram. Find the area of the triangle. Area properties. oral exercises. Find the area of the parallelogram. Parallelogram heights. Find the perimeter of the square. Area of a triangle. Find the area of the square. Find the area of the rectangle. Square area.
“Kvadrat 8th grade” - Black square. Tasks for oral work around the perimeter of the square. Square area. Square signs. The square is among us. A square is a rectangle with all sides equal. Square. Bag with a square base. oral tasks. How many squares are shown in the picture. Square properties. Wealthy merchant. Tasks for oral work on the area of the square. The perimeter of a square.
"Definition of axial symmetry" - Points lying on the same perpendicular. Draw two lines. Construction. Plot points. Clue. Figures that do not have axial symmetry. Section. Missing coordinates. Figure. Shapes that have more than two axes of symmetry. Symmetry. Symmetry in poetry. Build triangles. Axes of symmetry. Building a segment. Building a point. Figures with two axes of symmetry. Peoples. Triangles. Proportionality.
"Defining Similar Triangles" - Polygons. proportional cuts. The ratio of the areas of similar triangles. Two triangles are called similar. Conditions. Construct a triangle given two angles and the bisector at the vertex. Suppose we need to determine the distance to the pole. The third sign of the similarity of triangles. Let's build a triangle. ABC. Triangles ABC and ABC have three equal sides. Determining the height of an object.
"Solution of the Pythagorean theorem" - Parts of windows. The simplest proof. Hammurabi. Diagonal. Complete proof. Proof by subtraction. Pythagoreans. Proof by decomposition method. History of the theorem. Diameter. Proof by the complement method. Epstein's proof. Cantor. Triangles. followers. Applications of the Pythagorean theorem. Pythagorean theorem. Statement of the theorem. Proof of Perigal. Application of the theorem.
Sign of similarity of right triangles
Let us first introduce the sign of similarity of right-angled triangles.
Theorem 1
Sign of similarity of right triangles: two right-angled triangles are similar when they have one equal acute angle each (Fig. 1).
Figure 1. Similar Right Triangles
Proof.
Let us be given that $\angle B=\angle B_1$. Since the triangles are right-angled, $\angle A=\angle A_1=(90)^0$. Therefore, they are similar according to the first sign of the similarity of triangles.
The theorem has been proven.
Height theorem in a right triangle
Theorem 2
The height of a right triangle drawn from the vertex of the right angle divides the triangle into two similar right triangles, each of which is similar to the given triangle.
Proof.
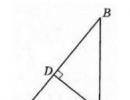
Let us be given a right triangle $ABC$ with right angle $C$. Draw the height $CD$ (Fig. 2).

Figure 2. Illustration of Theorem 2
Let us prove that triangles $ACD$ and $BCD$ are similar to triangle $ABC$ and that triangles $ACD$ and $BCD$ are similar.
Since $\angle ADC=(90)^0$, the triangle $ACD$ is right-angled. Triangles $ACD$ and $ABC$ have common angle $A$, therefore, by Theorem 1, triangles $ACD$ and $ABC$ are similar.
Since $\angle BDC=(90)^0$, the triangle $BCD$ is right-angled. Triangles $BCD$ and $ABC$ have common angle $B$, therefore, by Theorem 1, triangles $BCD$ and $ABC$ are similar.
Consider now the triangles $ACD$ and $BCD$
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]
Therefore, by Theorem 1, the triangles $ACD$ and $BCD$ are similar.
The theorem has been proven.
Average proportional
Theorem 3
The height of a right triangle, drawn from the vertex of the right angle, is the average proportional for the segments into which the height divides the hypotenuse of this triangle.
Proof.
By Theorem 2, we have that the triangles $ACD$ and $BCD$ are similar, therefore
The theorem has been proven.
Theorem 4
The leg of a right triangle is the mean proportional between the hypotenuse and the segment of the hypotenuse enclosed between the leg and the height drawn from the vertex of the angle.
Proof.
In the proof of the theorem, we will use the notation from Figure 2.
By Theorem 2, we have that the triangles $ACD$ and $ABC$ are similar, hence
The theorem has been proven.
Sign of similarity of right triangles
Let us first introduce the sign of similarity of right-angled triangles.
Theorem 1
Sign of similarity of right triangles: two right-angled triangles are similar when they have one equal acute angle each (Fig. 1).
Figure 1. Similar Right Triangles
Proof.
Let us be given that $\angle B=\angle B_1$. Since the triangles are right-angled, $\angle A=\angle A_1=(90)^0$. Therefore, they are similar according to the first sign of the similarity of triangles.
The theorem has been proven.
Height theorem in a right triangle
Theorem 2
The height of a right triangle drawn from the vertex of the right angle divides the triangle into two similar right triangles, each of which is similar to the given triangle.
Proof.
Let us be given a right triangle $ABC$ with right angle $C$. Draw the height $CD$ (Fig. 2).

Figure 2. Illustration of Theorem 2
Let us prove that triangles $ACD$ and $BCD$ are similar to triangle $ABC$ and that triangles $ACD$ and $BCD$ are similar.
Since $\angle ADC=(90)^0$, the triangle $ACD$ is right-angled. Triangles $ACD$ and $ABC$ have common angle $A$, therefore, by Theorem 1, triangles $ACD$ and $ABC$ are similar.
Since $\angle BDC=(90)^0$, the triangle $BCD$ is right-angled. Triangles $BCD$ and $ABC$ have common angle $B$, therefore, by Theorem 1, triangles $BCD$ and $ABC$ are similar.
Consider now the triangles $ACD$ and $BCD$
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]
Therefore, by Theorem 1, the triangles $ACD$ and $BCD$ are similar.
The theorem has been proven.
Average proportional
Theorem 3
The height of a right triangle, drawn from the vertex of the right angle, is the average proportional for the segments into which the height divides the hypotenuse of this triangle.
Proof.
By Theorem 2, we have that the triangles $ACD$ and $BCD$ are similar, therefore
The theorem has been proven.
Theorem 4
The leg of a right triangle is the mean proportional between the hypotenuse and the segment of the hypotenuse enclosed between the leg and the height drawn from the vertex of the angle.
Proof.
In the proof of the theorem, we will use the notation from Figure 2.
By Theorem 2, we have that the triangles $ACD$ and $ABC$ are similar, hence
The theorem has been proven.
Lesson Objectives:
- introduce the concept of the mean proportional (geometric mean) of two segments;
- consider the problem of proportional segments in a right triangle: a property of the height of a right triangle drawn from the vertex of a right angle;
- to form students' skills in using the studied topic in the process of solving problems.
Lesson type: lesson learning new material.
Plan:
- Organizational moment.
- Knowledge update.
- Studying the property of the height of a right triangle drawn from the vertex of a right angle:
- preparatory stage;
– introduction;
- assimilation. - Introduction of the concept of mean proportional to two segments.
- Assimilation of the concept of the average proportional of two segments.
- Proof of the consequences:
- the height of a right triangle, drawn from the vertex of the right angle, is the average proportional between the segments into which the hypotenuse is divided by this height;
- the leg of a right triangle is the mean proportional between the hypotenuse and the segment of the hypotenuse enclosed between the leg and the height. - Problem solving.
- Summarizing.
- Setting homework.
During the classes
I. ORGANIZATION
Hello guys, have a seat. Is everyone ready for the lesson?
We start work.
II. UPDATE OF KNOWLEDGE
What important mathematical concept did you learn in previous lessons? ( with the concept of triangle similarity)
- Let's remember which two triangles are called similar? (two triangles are called similar if their angles are respectively equal and the sides of one triangle are proportional to the similar sides of the other triangle)
What do we use to prove the similarity of two triangles? (
- List these signs. (formulate three signs of similarity of triangles)
III. STUDYING THE PROPERTIES OF THE HEIGHT OF A RECTANGULAR TRIANGLE CARRIED OUT FROM THE VERTEX OF A RIGHT ANGLE
a) preparatory stage
- Guys, please look at the first slide. ( Appendix) Here are two right-angled triangles - and . and are the heights and, respectively. ![]() .
.
Task 1. a) Determine if and are similar.
What do we use to prove the similarity of triangles? ( signs of similarity of triangles)
(the first sign, since nothing is known about the sides of triangles in the problem)
. (Two pairs: 1. ∟B= ∟B1 (straight lines), 2. ∟A= ∟A 1)
- Make a conclusion. ( by the first sign of similarity of triangles ~)
Task 1. b) Determine if and are similar.
What similarity criterion will we use and why? (the first sign, because in the problem nothing is known about the sides of triangles)
How many pairs of equal angles do we need to find? Find these couples (because the triangles are right-angled, one pair of equal angles is enough: ∟A= ∟A 1)
- Make a conclusion. (by the first sign of similarity of triangles, we conclude that these triangles are similar).
As a result of the conversation, slide 1 looks like this:

b) discovery of the theorem
Task 2.
Determine if and , and are similar. As a result of the conversation, answers are built, which are reflected on the slide.

- The figure indicated that . Did we use this degree measure when answering the questions of tasks? ( No, not used)
- Guys, draw a conclusion: into which triangles does the height drawn from the vertex of the right angle divide the right triangle? (make a conclusion)

- The question arises: will these two right-angled triangles, into which the height divides the right-angled triangle, be similar to each other? Let's try to find pairs of equal angles.
As a result of the conversation, a record is built:

- And now let's make a full conclusion. ( CONCLUSION: the height of a right triangle drawn from the vertex of the right angle divides the triangle into two similar
- That. we have formulated and proved a theorem on the property of the height of a right triangle.
Let's establish the structure of the theorem and make a drawing. What is given in the theorem and what needs to be proved? Students write in their notebooks:

Let's prove the first point of the theorem for the new drawing. What similarity criterion will we use and why? (First, since nothing is known about the sides of triangles in the theorem)
How many pairs of equal angles do we need to find? Find these couples. (In this case, one pair is enough: ∟A-general)
- Make a conclusion. The triangles are similar. As a result, an example of the formulation of the theorem is shown

- Write the second and third points at home yourself.
c) assimilation of the theorem
- So, formulate the theorem again (The height of a right triangle, drawn from the vertex of the right angle, divides the triangle into two similar right-angled triangles, each of which is similar to this one)
- How many pairs of similar triangles in the construction "in a right triangle the height from the vertex of a right angle" can be found by this theorem? ( Three couples)
Students are given the following assignment:

IV. INTRODUCTION OF THE CONCEPT OF THE AVERAGE PROPORTIONAL OF TWO LINES
Now we are going to learn a new concept.
Attention!
Definition. Section XY called average proportional (geometric mean) between segments AB and CD, if
(write in notebook).
V. ASSOCIATION OF THE CONCEPT OF THE AVERAGE PROPORTIONAL OF TWO LINES
Now let's move on to the next slide.
Exercise 1. Find the length of the average proportional segments MN and KP, if MN = 9 cm, KP = 16 cm.
- What is given in the task? ( Two segments and their lengths: MN = 9 cm, KP = 16 cm)
- What do you need to find? ( The length of the average proportional of these segments)
- What is the formula for the mean proportional and how do we find it?
(We substitute the data into the formula and find the length of the mean prop.)
Task number 2. Find the length of segment AB if the average proportional of segments AB and CD is 90 cm and CD = 100 cm
- What is given in the task? (the length of the segment CD = 100 cm and the average proportional of the segments AB and CD is 90 cm)
What should be found in the problem? ( Length of segment AB)
- How are we going to solve the problem? (Let's write down the formula for the average proportional segments AB and CD, express the length of AB from it and substitute the data of the problem.)
VI. CONCLUSION
- Well done boys. And now let's return to the similarity of triangles, proved by us in the theorem. Restate the theorem. ( The height of a right triangle drawn from the vertex of the right angle divides the triangle into two similar right triangles, each of which is similar to a given)
- Let's first use the similarity of triangles and . What follows from this? ( By definition of similarity, sides are proportional to similar sides)
- What equality will be obtained when using the basic property of proportion? ()
– Express CD and draw a conclusion (![]() ;
;![]() .
.
Conclusion: the height of a right triangle, drawn from the vertex of the right angle, is the average proportional between the segments into which the hypotenuse is divided by this height)
- And now prove for yourself that the leg of a right triangle is the average proportional between the hypotenuse and the segment of the hypotenuse enclosed between the leg and the height. We find from - ... the segments into which the hypotenuse is divided by this height )
The leg of a right triangle is the mean proportional between ... (- ... the hypotenuse and the segment of the hypotenuse enclosed between this leg and the height )
– Where do we apply the learned statements? ( When solving problems)
IX. SETTING HOMEWORK
d/z: No. 571, No. 572 (a, e), independent work in a notebook, theory.
Today, your attention is invited to another presentation on an amazing and mysterious subject - geometry. In this presentation, we will introduce you to a new property of geometric shapes, in particular, the concept of proportional segments in right triangles.
First you need to remember what is a triangle? This is the simplest polygon, consisting of three vertices connected by three segments. A right triangle is a triangle in which one of the angles is 90 degrees. You have already got acquainted with them in more detail in our previous training materials presented to your attention.
So, returning to our topic today, we denote in order that the height of a right-angled triangle, drawn from an angle of 90 degrees, divides it into two triangles, which are similar both to each other and to the original one. All the drawings and graphs you are interested in are given in the proposed presentation, and we recommend that you refer to them, accompanying the described explanation.
A graphical example of the above thesis can be seen on the second slide. Triangles are similar because they have two identical angles. If you specify in more detail, then the height lowered to the hypotenuse forms a right angle with it, that is, there are already identical angles, and each of the formed angles also has one common angle as its original. The result is two angles equal to each other. That is, the triangles are similar.

Let us also denote what the concept of “mean proportional” or “geometric mean” means by itself? This is a certain XY segment for segments AB and CD when it is equal to the square root of the product of their lengths.
From which it also follows that the leg of a right triangle is the geometric mean between the hypotenuse and the projection of this leg onto the hypotenuse, that is, the other leg.

Another property of a right triangle is that its height, drawn from an angle of 90 o, is the average proportional between the projections of the legs onto the hypotenuse. If you refer to the presentation and other materials brought to your attention, you will see that there is a proof of this thesis in a very simple and accessible form. Earlier we have already proved that the resulting triangles are similar to each other and to the original triangle. Then, using the ratio of the legs of these geometric figures, we come to the conclusion that the height of a right triangle is directly proportional to the square root of the product of the segments that were formed as a result of lowering the height from the right angle of the original triangle.

The last thing in the presentation is that the leg of a right triangle is the geometric mean for the hypotenuse and its segment located between the leg and the height drawn from an angle equal to 90 degrees. This case should be considered from the side that these triangles are similar to each other, and the leg of one of them is obtained by the hypotenuse of the other. But you will get to know this in more detail by studying the proposed materials.