Algoritmul metodei Simplex. Metoda simplă pentru rezolvarea zlp. Problemă de programare liniară condiționată standard

Dacă trebuie să rezolvați o problemă de programare liniară folosind tabele simplex, atunci serviciul nostru online vă va fi de mare ajutor. Metoda simplex implică o enumerare secvențială a tuturor vârfurilor din intervalul de valori admisibile pentru a găsi vârful în care funcția ia o valoare extremă. În prima etapă, se găsește o soluție, care este îmbunătățită la fiecare etapă ulterioară. Această soluție se numește de bază. Iată o succesiune de acțiuni la rezolvarea unei probleme de programare liniară utilizând metoda simplex:

Primul pas. În tabelul compilat, în primul rând, trebuie să vă uitați la coloana cu membri liberi. Dacă există elemente negative în el, atunci este necesar să treceți la al doilea pas, dacă nu, apoi la al cincilea.

Al doilea pas. La al doilea pas, este necesar să decidem ce variabilă să excludem de la bază și care să includem, pentru a recalcula tabelul simplex. Pentru a face acest lucru, căutați prin coloană cu membri liberi și găsiți un element negativ în ea. Linia cu un element negativ se va numi linia principală. În el găsim elementul negativ maxim în valoare absolută, coloana corespunzătoare - următorul. Dacă există valori negative între membrii liberi, dar nu în rândul corespunzător, atunci un astfel de tabel nu va avea soluții. Prin schimbarea în primul rând, cel din coloana membrilor liberi este exclus din bază, iar variabila corespunzătoare coloanei principale este inclusă în bază.

Tabelul 1.

variabile de bază	Membri liberi în constrângeri	Variabile non-bazice
variabile de bază	Membri liberi în constrângeri	x 1	x 2	...	x l	...	x n
x n + 1	b 1	a 11	a 12	...	un 1l	...	un 1n
x n + 2	b 2	a 21	a 22	...	un 2l	...	un 2n
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n + r	b2	a r1	a r2	...	a rl	...	un rn
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n + m	b m	un m1	un m2	...	un ml	...	un mn
F (x) max	F 0	-c 1	-c 2	...	-c 1	...	-c n

Al treilea pas. La al treilea pas, recalculăm întregul tabel simplex folosind formule speciale, aceste formule pot fi văzute folosind.

Al patrulea pas. Dacă, după recalculare, elementele negative rămân în coloana membrilor liberi, treceți la primul pas, dacă nu există astfel, atunci la al cincilea.

Al cincilea pas. Dacă ați atins al cincilea pas, atunci ați găsit o soluție care este acceptabilă. Cu toate acestea, acest lucru nu înseamnă că este optim. Va fi optim numai dacă toate elementele din rândul F sunt pozitive. Dacă nu este cazul, atunci este necesar să îmbunătățim soluția, pentru care găsim rândul și coloana principală pentru următorul recalcul în conformitate cu următorul algoritm. Inițial, găsim numărul negativ minim în linia F, excluzând valoarea funcției. Coloana cu acest număr va fi prima. Pentru a găsi rândul principal, găsim raportul dintre membrul liber corespunzător și elementul din coloana principală, cu condiția să fie pozitive. Relația minimă vă va permite să definiți rândul principal. Recalculăm din nou tabelul folosind formulele, adică treceți la pasul 3.

Iată o soluție manuală (nu un applet) a două probleme prin metoda simplex (similară cu soluția unui applet) cu explicații detaliate pentru a înțelege algoritmul pentru rezolvarea problemelor folosind metoda simplex. Prima problemă conține doar semne de inegalitate "≤" (o problemă cu o bază inițială), a doua poate conține semne "≥", "≤" sau "=" (o problemă cu o bază artificială), sunt rezolvate în moduri diferite .

Metoda Simplex, rezolvarea unei probleme cu o bază inițială

1)Metoda Simplex pentru o problemă cu o bază inițială (toate semnele constrângerilor de inegalitate „≤”).

Să scriem sarcina în canonic formă, adică constrângerile inegalității pot fi rescrise ca egalități prin adăugare bilanț variabile:

Acest sistem este un sistem cu o bază (baza s 1, s 2, s 3, fiecare dintre ele este inclusă într-o singură ecuație a sistemului cu coeficientul 1), x 1 și x 2 sunt variabile libere. Problemele, în soluția cărora se utilizează metoda simplex, trebuie să aibă următoarele două proprietăți: - sistemul de constrângeri trebuie să fie un sistem de ecuații cu o bază; - termenii liberi ai tuturor ecuațiilor din sistem trebuie să fie negativi.

Sistemul rezultat este un sistem cu o bază și termenii săi liberi nu sunt negativi; prin urmare, putem aplica metoda simplex... Să alcătuim primul tabel simplex (Iterarea 0) pentru a rezolva problema metoda simplex, adică un tabel al coeficienților funcției obiective și un sistem de ecuații pentru variabilele corespunzătoare. Aici "BP" înseamnă coloana variabilelor de bază, "Soluție" - coloana din partea dreaptă a ecuațiilor sistemului. Soluția nu este optimă pentru că există coeficienți negativi în rândul z.

iterația metodei simplex 0

							Atitudine

Pentru a îmbunătăți soluția, să trecem la următoarea iterație metoda simplex, obținem următorul tabel simplex. Pentru a face acest lucru, trebuie să alegeți coloana permisivă, adică o variabilă care va fi inclusă în bază la următoarea iterație a metodei simplex. Este selectat de cel mai mare coeficient negativ în valoare absolută în rândul z (în problema maximă) - în iterația inițială a metodei simplex, aceasta este coloana x 2 (coeficient -6).

Este apoi selectat șir permisiv, adică variabila care va ieși din bază la următoarea iterație a metodei simplex. Este selectat de cel mai mic raport dintre coloana „Decizie” și elementele pozitive corespunzătoare ale coloanei de rezolvare (coloana „Raport”) - în iterația inițială, acesta este rândul s 3 (coeficientul 20).

Element permisiv este situat la intersecția coloanei de rezolvare și a rândului de rezolvare, celula sa este evidențiată, este egală cu 1. Prin urmare, la următoarea iterație a metodei simplex, variabila x 2 va fi înlocuită în baza s 1. Rețineți că relația nu este căutată în linia z; o liniuță "-" este pusă acolo. Dacă există relații minime identice, atunci se alege oricare dintre ele. Dacă în coloana de rezolvare toți coeficienții sunt mai mici sau egali cu 0, atunci soluția problemei este infinită.

Să completăm următorul tabel „Iterarea 1”. O vom obține din tabelul „Iterarea 0”. Scopul transformărilor ulterioare este de a transforma coloana de rezolvare x 2 într-una (cu unul în loc de elementul de rezolvare și zerouri în loc de alte elemente).

1) Calculul rândului x 2 al tabelului "Iterarea 1". În primul rând, împărțim toți membrii rândului de rezolvare s 3 al tabelului "Iterarea 0" la elementul de rezolvare (este egal cu 1 în acest caz) din acest tabel, obținem rândul x 2 în tabelul Iterarea 1. pentru că elementul de rezolvare în acest caz este egal cu 1, apoi rândul s 3 al tabelului "Iterarea 0" va coincide cu rândul x 2 al tabelului "Iterarea 1". Am primit rândul x 2 al tabelului "Iterarea 1" 0 1 0 0 1 20, restul rândurilor din tabelul "Iterarea 1" vor fi obținute din acest rând și rândurile tabelului "Iterarea 0" după cum urmează:

2) Calculul rândului z al tabelului "Iterarea 1". În locul lui -6 în primul rând (rândul z) din coloana x 2 a tabelului Iteration 0, ar trebui să existe 0 în primul rând al tabelului Iteration 1. Pentru a face acest lucru, înmulțim toate elementele rândului x 2 din tabelul „Iterare 1” 0 1 0 0 1 20 cu 6, obținem 0 6 0 0 6 120 și adăugăm acest rând cu primul rând (z - rând) de tabelul „Iterare 0” -4 -6 0 0 0 0, obținem -4 0 0 0 6 120. În coloana x 2, apare zero 0, obiectivul este atins. Elementele permisive ale coloanei x 2 sunt evidențiate cu roșu.

3) Calculul rândului s 1 al tabelului "Iterarea 1". În locul 1 din rândul 1 al tabelului "Iterare 0", trebuie să existe 0 în tabelul "Iterare 1". Pentru a face acest lucru, înmulțim toate elementele rândului x 2 din tabelul „Iterare 1” 0 1 0 0 1 20 cu -1, obținem 0 -1 0 0 -1 -20 și adăugăm acest rând cu s 1 - rândul din tabelul „Iterare 0” 2 1 1 0 0 64, obținem rândul 2 0 1 0 -1 44. În coloana x 2 obținem 0 necesar.

4) Calculul rândului 2 al tabelului "Iterarea 1". În locul 3 din rândul 2 al tabelului "Iterare 0", trebuie să fie 0 în tabelul "Iterare 1". Pentru a face acest lucru, înmulțim toate elementele rândului x 2 din tabelul „Iterarea 1” 0 1 0 0 1 20 cu -3, obținem 0 -3 0 0 -3 -60 și adăugăm acest rând cu s 1 - rândul tabelului "Iterare 0" 1 3 0 1 0 72, obținem rândul 1 0 0 1 -3 12. În coloana x 2, se obține 0 dorit. Coloana x 2 din tabelul "Iterarea 1" a devenit una , conține unul 1 și restul 0.

Rândurile din tabelul „Iterarea 1” se obțin conform următoarei reguli:

Rând Nou = Rând Vechi - (Factor Coloană Rezoluție Rând Vechi) * (Rând Nou Rezoluție).

De exemplu, pentru linia z avem:

Linie z veche (-4 -6 0 0 0 0) - (- 6) * Linie nouă de rezolvare - (0 -6 0 0 -6 -120) = Linie z nouă (-4 0 0 0 6 120).

Pentru următoarele tabele, recalcularea elementelor de tabel se face în același mod, așa că o omitem.

iterația metodei simplex 1

							Atitudine

Permiterea coloanei x 1, rezolvarea rândului s 2, s 2 părăsește baza, x 1 intră în bază. Exact în același mod, obținem restul tabelelor simplex până când obținem un tabel cu toți coeficienții pozitivi în rândul z. Acesta este semnul unui tabel optim.

iterația metodei simplex 2

							Atitudine

Coloana de rezolvare s 3, rândul de rezolvare s 1, s 1 părăsește baza, s 3 intră în bază.

iterația metodei simplex 3

							Atitudine

În rândul z, toți coeficienții sunt negativi, prin urmare, soluția optimă se obține x 1 = 24, x 2 = 16, z max = 192.

Programare liniară este o tehnică de modelare matematică concepută pentru a optimiza utilizarea resurselor limitate. Medicamentul a fost utilizat cu succes în domeniul militar, industrial, agricol, transport, economie, îngrijire a sănătății și chiar în științele sociale. Utilizarea pe scară largă a acestei metode este, de asemenea, susținută de algoritmi de calculator extrem de eficienți care implementează această metodă. Algoritmii de optimizare pentru alte tipuri mai complexe de modele și probleme de cercetare operațională (IO), inclusiv programarea întreagă, neliniară și stocastică, se bazează pe algoritmi de programare liniară.

Sarcină de optimizare Este o problemă economică și matematică, care constă în găsirea valorii optime (maxime sau minime) a funcției obiective, iar valorile variabilelor trebuie să aparțină unui anumit interval de valori admisibile.

În forma sa cea mai generală, o problemă de programare liniară este scrisă matematic după cum urmează:

Unde X = (x 1 , X 2 , ..., X n ) ; W- gama de valori admisibile a variabilelor X 1 , X 2 , ..., X n ;f (X)- funcție obiectivă.

Pentru a rezolva problema de optimizare, este suficient să găsim soluția sa optimă, adică indicați astfel încât pentru orice.

O problemă de optimizare este de nerezolvat dacă nu are o soluție optimă. În special, problema de maximizare va fi de nerezolvat dacă funcția obiectivă f (X) nelimitată mai sus pe setul admisibil W.

Metodele de rezolvare a problemelor de optimizare depind atât de tipul funcției obiective f (X), și asupra structurii setului admisibil W... Dacă funcția obiectivă din problemă este o funcție n variabile, atunci metodele de soluție se numesc metode de programare matematică.

Trăsăturile caracteristice ale problemelor de programare liniară sunt următoarele:

indicator de optimitate f (X) este o funcție liniară a elementelor soluției X = (x 1 , X 2 , ..., X n ) ;

condițiile restrictive impuse soluțiilor posibile sunt sub formă de egalități sau inegalități liniare.

Problemă de programare liniară este sarcina cercetării operaționale, al cărei model matematic are forma:

(2) (3) (4) (5)

În acest caz, sistemul de ecuații liniare (3) și inegalități (4), (5), care determină setul admisibil de soluții la problemă W se numește sistem de restricții probleme de programare liniară și funcția liniară f (X) numit funcția țintă sau criteriul de optimitate .

O soluție valabilă Este o colecție de numere ( plan ) X = (X 1 , X 2 , ... , X n ) satisfacerea constrângerilor problemei. Soluție optimă Este un plan în care funcția obiectivă își ia valoarea maximă (minimă).

Dacă modelul matematic al problemei de programare liniară are forma:

apoi spun că problema este prezentată în formă canonică .

Orice problemă de programare liniară poate fi redusă la o problemă de programare liniară în formă canonică. Pentru a face acest lucru, în cazul general, trebuie să puteți reduce problema maximizării la problema minimizării; trece de la constrângeri de inegalitate la constrângeri de egalitate și înlocuiește variabilele care nu respectă condiția de non-negativitate. Maximizarea unor funcții este echivalentă cu minimizarea aceleiași funcții, luată cu semnul opus, și invers.

Regula pentru reducerea unei probleme de programare liniară la forma canonică este următoarea:

dacă în problema inițială este necesar să se determine maximul unei funcții liniare, atunci ar trebui să schimbați semnul și să căutați minimul acestei funcții;

dacă partea dreaptă a constrângerilor este negativă, atunci această constrângere ar trebui să fie înmulțită cu -1;

dacă există inegalități între constrângeri, atunci prin introducerea unor variabile suplimentare non-negative acestea se transformă în egalități;

dacă unele variabile X j nu are restricții de semn, apoi este înlocuit (în funcția obiectivă și în toate restricțiile) de diferența dintre două noi variabile non-negative: X 3 = x 3 + - X 3 - Unde X 3 + , X 3 - ≥ 0 .

Exemplul 1... Reducerea problemei de programare liniară la forma canonică:

min L = 2x 1 + x 2 - X 3 ; 2x 2 - X 3 ≤ 5; X 1 + x 2 - X 3 ≥ -1; 2x 1 - X 2 ≤ -3; X 1 ≤ 0; X 2 ≥ 0; X 3 ≥ 0.

Introducem în fiecare ecuație a sistemului de constrângeri variabilele de nivelare X 4 , X 5 , X 6 ... Sistemul va fi scris sub formă de egalități, iar în prima și a treia ecuație a sistemului de restricții variabilele X 4 , X 6 sunt introduse în partea stângă cu semnul "+", iar în a doua ecuație variabila X 5 este introdus cu un semn "-".

2x 2 - X 3 + x 4 = 5; X 1 + x 2 - X 3 - X 5 = -1; 2x 1 - X 2 + x 6 = -3; X 4 ≥ 0; X 5 ≥ 0; X 6 ≥ 0.

Termenii liberi în formă canonică trebuie să fie pozitivi, pentru aceasta înmulțim ultimele două ecuații cu -1:

2x 2 - X 3 + x 4 = 5; -X 1 - X 2 + x 3 + x 5 = 1; -2x 1 + x 2 - X 6 = 3.

Metoda Simplex pentru rezolvarea problemelor de programare liniară.

Algoritmul metodei simplex găsește soluția optimă luând în considerare un număr limitat de soluții de bază admisibile. Algoritmul metodei simplex începe întotdeauna cu o soluție de bază fezabilă și apoi încearcă să găsească o altă soluție de bază fezabilă care „îmbunătățește” valoarea funcției obiective. Acest lucru este posibil numai dacă o creștere a oricărei variabile zero (non-de bază) duce la o îmbunătățire a valorii funcției obiective. Dar pentru ca variabila non-de bază să devină pozitivă, una dintre variabilele de bază curente trebuie să fie zero, adică convertiți în non-de bază. Acest lucru este necesar pentru ca noua soluție să conțină exact m variabile de bază. În conformitate cu terminologia metodei simplex, se numește variabila zero selectată introdus (la bază), iar variabila de bază eliminată este exclus (de la bază).

Se vor numi două reguli pentru alegerea variabilelor introduse și excluzive în metoda simplex condiție de optimitate și condiția de admisibilitate ... Să formulăm aceste reguli și să luăm în considerare și secvența acțiunilor efectuate atunci când implementăm metoda simplex.

Stare de optimitate. Variabila introdusă în problema de maximizare (minimizare) este o variabilă fără bază având cel mai mare coeficient negativ (pozitiv) în ţintă-şir. Dacă intră ţintă-string are mai mulți astfel de coeficienți, atunci alegerea variabilei de intrare se face în mod arbitrar. Soluția optimă se obține atunci când se află ţintă-string, toți coeficienții variabilelor non-de bază vor fi non-negative (ne-pozitive).

Condiția de admisibilitate. Atât în problema maximizării, cât și în problema minimizării, variabila de bază este aleasă ca fiind cea exclusă, pentru care raportul dintre valoarea părții din dreapta a constrângerii și coeficientul pozitiv al coloanei de întâmpinare este minim. Dacă există mai multe variabile de bază cu această proprietate, atunci alegerea variabilei excluse se efectuează în mod arbitrar.

Să prezentăm un algoritm pentru rezolvarea problemei de programare liniară pentru găsirea maximului folosind tabele simplex.

F = s 1 x 1 + s 2 x 2 +… + s n x n max

x 1 0, x 2 0,…, x n 0.

Primul pas... Introducem variabile suplimentare și scriem sistemul de ecuații rezultat și funcția liniară sub forma unui sistem extins.

F - c 1 x 1 –c 2 x 2 - ... –c n x n = 0 = c p.

Al 2-lea pas. Asamblarea unui tabel simplex inițial.

Variabile	Variabile de bază și auxiliare	membri liberi (decizie)	Estimat atitudine
Variabile		membri liberi (decizie)	Estimat atitudine

Pasul 3. Verificăm îndeplinirea criteriului de optimitate - prezența coeficienților negativi în ultima linie. Dacă nu există astfel, soluția este optimă și F * = co, variabilele de bază sunt egale cu coeficienții corespunzători bj, variabilele non-de bază sunt egale cu zero, adică X * = (b 1, b 2, ..., bm , 0,…, 0).

Al 4-lea pas... Dacă criteriul de optimitate nu este îndeplinit, atunci cel mai mare coeficient negativ în valoare absolută din ultimul rând (estimat) determină coloana de rezolvare.

Pentru a determina linia de rezolvare, calculăm rapoartele estimate și completați ultima coloană a tabelului.

Raportul estimat al rândului I este

 dacă b i și a au semne diferite;

О dacă b i = 0 și а este<0;

 dacă a este = 0;

0 dacă b i = 0 și a este> 0;

În coloana relațiilor de valoare, găsim elementul minim min care definește șirul permisiv g.

Dacă nu există un minim, atunci problema nu are un I finit optim și este de nerezolvat.

La intersecția rândului și coloanei de rezolvare se află elementul de rezolvare a gs.

Al 5-lea pas... Construim următorul tabel. Pentru aceasta

Să trecem la al treilea pas.

Metoda M Uneori, atunci când se rezolvă LPP în matricea coeficienților cu sisteme necunoscute de constrângeri, nu există coloane unitare din care este posibil să se compună o matrice unitară, adică apare problema alegerii variabilelor de bază sau soluția inițială este invalidă. În astfel de cazuri, utilizați metoda bazei artificiale (metoda M). Se introduc toate constrângerile în care nu există variabile de bază variabile artificiale. Variabilele artificiale sunt introduse în funcția obiectivă cu un coeficient (- М) pentru problemele maxime și cu un coeficient (+ М) pentru problemele min, unde М este un număr pozitiv suficient de mare... Apoi problema extinsă este rezolvată conform regulilor metodei simplex. Dacă toate variabilele artificiale sunt egale cu zero, adică sunt excluse din bază, atunci fie se va obține o soluție optimă la problema inițială, fie problema inițială este rezolvată în continuare și se găsește soluția sa optimă, fie se stabilește indecidabilitatea ei. Dacă cel puțin una dintre variabilele artificiale se dovedește a fi nulă, atunci problema inițială nu are nicio soluție

Metoda universală de rezolvare a problemelor LP se numește metoda simplex. Aplicarea acestei metode și cea mai comună modificare a acesteia - metoda simplex în două faze.

În metoda grafică pentru rezolvarea problemelor LP, am ales de fapt din setul de vârfuri aparținând limitei setului de soluții la sistemul de inegalități un astfel de vârf la care valoarea funcției obiective a atins maximul (minim). În cazul a două variabile, această metodă este complet intuitivă și vă permite să găsiți rapid o soluție la problemă.

Dacă există trei sau mai multe variabile în problemă, iar în problemele economice reale aceasta este exact situația, este dificil de vizualizat zona soluțiilor la sistemul de constrângeri. Astfel de sarcini sunt rezolvate folosind metoda simplex sau prin metoda ameliorării succesive. Ideea metodei este simplă și este următoarea.

Conform unei anumite reguli, se găsește planul de referință inițial (un anumit vârf al zonei de constrângere). Se verifică dacă planul este optim. Dacă da, atunci problema este rezolvată. Dacă nu, atunci mergeți la un alt plan îmbunătățit - la un alt vârf. valoarea funcției obiective pe acest plan (la acest vârf) este evident mai bună decât în precedentul. Algoritmul de tranziție este realizat folosind o etapă de calcul, care este scrisă convenabil sub formă de tabele, numită tabele simplex ... Deoarece numărul de vârfuri este finit, atunci într-un număr finit de pași ajungem la soluția optimă.

Să luăm în considerare metoda simplex folosind un exemplu specific al problemei întocmirii unui plan.

Rețineți din nou că metoda simplex este aplicabilă rezolvării problemelor canonice LP reduse la o formă specială, adică având o bază, laturi pozitive din dreapta și o funcție obiectivă exprimată în termeni de variabile non-de bază. Dacă sarcina nu este redusă la un formular special, atunci sunt necesari pași suplimentari, despre care vom vorbi mai târziu.

Să luăm în considerare problema unui plan de producție, după ce am construit anterior un model și l-am redus la o formă specială.

O sarcină.

Pentru fabricarea produselor DARși ÎN depozitul nu poate elibera mai mult de 80 de unități de materii prime. Mai mult, pentru fabricarea produsului DAR se consumă două unități și produse ÎN- o unitate de materii prime. Este necesară planificarea producției, astfel încât cel mai mare profit să fie asigurat dacă produsele DAR este necesar să se facă nu mai mult de 50 de bucăți și produse ÎN- nu mai mult de 40 de bucăți. Mai mult, profitul din vânzarea unui produs DAR- 5 ruble, și de la ÎN- 3 ruble.

Să construim un model matematic, indicând pentru X 1 număr de produse A din plan, pentru X 2 - numărul de produse ÎN... atunci sistemul de restricții va arăta astfel:

x 1 ≤50
x 2 ≤40
2x 1 + x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 + 3x 2 → max

Să aducem problema într-o formă canonică prin introducerea unor variabile suplimentare:

x 1 + x 3 = 50
x 2 + x 4 = 40
2x 1 + x 2 + x 5 = 80
x 1 ≥0, x 2 ≥0
5x 1 + 3x 2 → max
-F = -5x 1 - 3x 2 → min.

Această problemă are o formă specială (cu o bază, laturile din dreapta sunt non-negative). Poate fi rezolvat folosind metoda simplex.

Euetapă. Scrierea unei probleme pe un tabel simplex. Există o corespondență unu-la-unu între sistemul de constrângeri al problemei (3.10) și tabelul simplex. Există atât de multe rânduri în tabel câte egalități există în sistemul de constrângeri și există atât de multe coloane câte variabile libere. Variabilele de bază umple prima coloană, variabilele libere umple rândul de sus al tabelului. Linia de jos se numește linia index; conține coeficienții variabilelor din funcția obiectivă. Inițial, 0 este scris în colțul din dreapta jos, dacă nu există un termen liber în funcție; dacă există, atunci o notăm cu semnul opus. În acest loc (în colțul din dreapta jos) va exista valoarea funcției obiective, care, atunci când se deplasează de la o masă la alta, ar trebui să crească în modul. Deci, sistemul nostru de restricții corespunde Tabelului 3.4 și putem trece la etapa II a soluției.

Tabelul 3.4

de bază			gratuit

IIetapă... Verificarea planului de asistență pentru optimitate.

Acest tabel 3.4 corespunde următorului plan de bază:

(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).

Variabile libere X 1 , X 2 sunt 0; X 1 = 0, X 2 = 0. Și variabilele de bază X 3 , X 4 , X 5 preia valorile X 3 = 50, X 4 = 40, X 5 = 80 - din coloana membrilor liberi. Valoarea funcției obiective:

-F = - 5X 1 - 3X 2 = -5 0 - 3 0 = 0.

Sarcina noastră este de a verifica dacă un anumit plan de bază este optim. pentru aceasta, trebuie să vizualizați linia index - linia funcției obiective F.

Sunt posibile diverse situații.

1. În index F-stringul nu are elemente negative. Aceasta înseamnă că planul este optim, puteți scrie soluția problemei. Funcția obiectivă și-a atins valoarea optimă egală cu numărul din colțul din dreapta jos luat cu semnul opus. Trecem la etapa IV.

2. Există cel puțin un element negativ în rândul index și nu există elemente pozitive în coloană. Apoi concluzionăm că funcția obiectivă F→ ∞ scade la infinit.

3. Rândul index conține un element negativ cu cel puțin un element pozitiv în coloana sa. Apoi trecem la etapa următoare III. recalculăm tabelul, îmbunătățind planul de bază.

IIIetapă... Îmbunătățirea liniei de bază.

Din elemente de index negative F-Rândurile aleg cel mai mare modul, apelează rezolvarea coloanei corespunzătoare și marchează „”.

Pentru a selecta rândul de rezolvare, este necesar să se calculeze rapoartele elementelor din coloana de membru liber numai la pozitiv elemente de coloană permisive. Alegeți minimul dintre relațiile obținute. Elementul corespunzător, la care se atinge minimul, se numește cel care rezolvă. Îl vom evidenția cu un pătrat.

În exemplul nostru, elementul 2 este permisiv. Linia corespunzătoare acestui element se mai numește rezolvare (Tabelul 3.5).

Tabelul 3.5

După ce am ales elementul de rezolvare, recalculăm tabelul conform regulilor:

1. În noul tabel cu aceeași dimensiune ca înainte, variabilele rândului și coloanei de rezolvare sunt schimbate, ceea ce corespunde tranziției la o nouă bază. În exemplul nostru: X 1 este inclus în bază, în loc de X 5, care lasă baza și este acum liber (Tabelul 3.6).

Tabelul 3.6

2. În locul elementului de rezolvare 2, scrieți numărul său invers ½.

3. Elementele liniei de rezolvare sunt împărțite la elementul de rezolvare.

4. Elementele coloanei de rezolvare sunt împărțite la elementul de rezolvare și sunt scrise cu semnul opus.

5. Pentru a completa restul elementelor din Tabelul 3.6, recalculăm conform regulii dreptunghiului. Să presupunem că vrem să numărăm elementul în poziția 50.

Conectăm mental acest element cu cel care rezolvă, găsim produsul, scădem produsul elementelor situate pe cealaltă diagonală a dreptunghiului rezultat. Împărțim diferența cu elementul de rezolvare.

Asa de, . Scriem 10 la locul unde erau 50. În mod similar:
, , , .

Tabelul 3.7

Avem un nou tabel 3.7, variabilele de bază sunt acum variabilele (x 3, x 4, x 1). Valoarea funcției obiective a devenit egală cu -200, adică scăzut. Pentru a verifica această soluție de bază pentru optimitate, este necesar să treceți din nou la etapa II. Procesul este evident finit, criteriile de oprire sunt punctele 1 și 2 din etapa II.

Să aducem soluția problemei până la capăt. Pentru a face acest lucru, verificați rândul index și, văzând în el un element negativ -½, apelați rezolvarea coloanei corespunzătoare și, conform etapei III, recalculați tabelul. După ce am compilat relațiile și am ales dintre ele minimul = 40, am determinat elementul de rezolvare 1. Acum efectuăm recalcularea conform regulilor 2-5.

Tabelul 3.8

După recalcularea tabelului, ne asigurăm că nu există elemente negative în rândul index, prin urmare, problema este rezolvată, planul de bază este optim.

IVetapă... Scrierea soluției optime.

Dacă metoda simplex s-a oprit conform punctului 1 al etapei II, atunci soluția problemei este scrisă după cum urmează. Variabilele de bază iau respectiv valorile coloanei membre libere. În exemplul nostru X 3 = 30, X 2 = 40, X 1 = 20. Variabilele libere sunt 0, X 5 = 0, X 4 = 0. Funcția obiectiv ia valoarea ultimului element al coloanei membrilor liberi cu semnul opus: - F = -220 → F= 220, în exemplul nostru, funcția a fost examinată pentru min și inițial F→ max, deci semnul s-a schimbat de două ori. Asa de, X* = (20, 40, 30, 0, 0), F* = 220. Răspuns la problemă:

Este necesar să includeți 20 de produse de acest tip DAR, 40 de produse de tip B, în timp ce profitul va fi maxim și va fi egal cu 220 de ruble.

La sfârșitul acestei secțiuni, vă prezentăm o diagramă bloc a algoritmului metodei simplex, care repetă exact pașii, dar, probabil, pentru unii cititori va fi mai convenabil de utilizat, deoarece săgețile indică o direcție clară de acțiune .

Legăturile de deasupra casetelor din diagrama de flux arată care etapă sau subclauză aparține grupului de transformare corespunzător. regula pentru găsirea planului inițial de bază va fi formulată în clauza 3.7.

Un exemplu. Rezolvați următoarea problemă LP în formă canonică folosind metoda simplex.
f (x) = x 1 + 9x 2 + 5x 3 + 3x 4 + 4x 5 + 14x 6 → min
x 1 + x 4 = 20
x 2 + x 5 = 50
x 3 + x 6 = 30
x 4 + x 5 + x 6 = 60
x i ≥ 0, i = 1, ..., 6
Ei spun că o problemă LP are o formă canonică dacă toate constrângerile (cu excepția condițiilor de negativitate a variabilelor) au forma egalităților și toți termenii liberi sunt non-negativi. Deci avem o problemă în formă canonică.
Ideea din spatele metodei simplex este următoarea. În primul rând, trebuie să găsiți un vârf (inițial) al poliedrului soluțiilor fezabile (soluția de bază fezabilă inițială). Apoi, trebuie să verificați această soluție pentru optimitate. Dacă este optim, atunci s-a găsit soluția; dacă nu, atunci mergeți la un alt vârf al politopului și verificați din nou optimitatea. Având în vedere finitudinea vârfurilor poliedrului (o consecință a limitării restricțiilor problemei LP) într-un număr finit de „pași” vom găsi punctul minim sau maxim necesar. Trebuie remarcat faptul că la trecerea de la un vârf la altul, valoarea funcției obiective scade (în problema pentru minim) sau crește (în problema pentru maxim).
Astfel, ideea metodei simplex se bazează pe trei proprietăți ale problemei LP.
Decizie. Pentru a găsi soluția inițială de bază fezabilă, adică pentru a determina variabilele de bază, sistemul (5.6) trebuie redus la o formă „diagonală”. Aplicând metoda Gauss (metoda eliminării succesive a necunoscutelor), obținem din (5.6):
x 2 + x 1 + x 3 = 40
x 4 + x 1 = 20
x 5 -x 1 -x 3 = 10
x 6 + x 3 = 30
Prin urmare, variabilele de bază sunt x 2, x 4, x 5, x 6, le atribuim valori egale cu membrii liberi ai șirurilor corespunzătoare: x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,... Variabile x 1și x 3 sunt non-de bază: x 1 = 0, x 3 = 0.
Să construim soluția de bază inițială admisibilă
x 0 = (0,40,0,20,10,30) (5,9)
Pentru a verifica optimitatea soluției găsite x 0 este necesar să se excludă variabilele de bază din funcția obiectivului (folosind sistemul (5.8)) și să se construiască un tabel simplex special.
După eliminarea variabilelor, este convenabil să scrieți funcția obiectivă în forma:
f (x) = -7x 1 - 14x 3 +880 (5.10)
Acum, folosind (5.8) - (5.10), alcătuim un tabel simplex inițial:

Linia zero conține coeficienții cu semnul opus al variabilelor corespunzătoare funcției obiective. Criteriul de optimitate (pentru problema găsirii unui minim): soluție de bază admisibilă ( x 0) este optim dacă linia zero nu conține niciun număr strict pozitiv (fără a se număra valoarea funcției obiective (880)). Această regulă se aplică și următoarelor iterații (tabele). Elementele rândului zero vor fi numite estimări ale coloanei.
Deci, soluția de bază admisibilă inițială (5.9) nu este optimă: 7>0, 14>0 .
Coloana zero conține valorile variabilelor de bază. Ele trebuie să fie non-negative (a se vedea ecuația (5.7)). De la primul până la al patrulea rând, se scriu coeficienții variabilelor din sistem (5.8).
La fel de x 0 nu este optim, atunci trebuie să mergeți la un alt vârf al poliedrului soluțiilor fezabile (construiți un nou b.d.). Pentru a face acest lucru, trebuie să găsiți pivotul și să efectuați o anumită transformare (transformare simplex).
În primul rând, găsim elementul principal al tabelului, care se află la intersecția coloanei principale (coloana cu cel mai mare scor pozitiv) și rândul principal (rândul corespunzător raportului minim dintre elementele coloanei zero la elementele corespunzătoare (strict pozitive) ale coloanei de întâmpinare).
În tabelul 1, coloana principală este a treia coloană, iar rândul principal este al patrulea rând. (min (40 / 1,30 / 1) = 30/1) sunt indicate de săgeți, iar elementul de conducere este indicat printr-un cerc. Gazda indică faptul că variabila de bază x 6 trebuie înlocuit cu un non-de bază x 3... Apoi, noile variabile de bază vor fi x 2, x 3, x 4, x 5,, și cele non-de bază - x 1, x 6,... Aceasta înseamnă o tranziție la un nou vârf al poliedrului soluțiilor fezabile. Pentru a găsi valorile coordonate ale noii soluții de bază fezabile x 00 trebuie să construiți un nou tabel simplex și să efectuați transformări elementare în acesta:
dar)împărțiți toate elementele liniei de conducere la elementul de conducere, transformând astfel elementul de conducere în 1 (pentru simplitatea calculelor);
b) folosind elementul principal (egal cu 1), transformați toate elementele coloanei principale în zerouri (similar cu metoda de eliminare a necunoscutelor);
Ca rezultat, în coloana zero se obțin valorile noilor variabile de bază x 2, x 3, x 4, x 5,(vezi tabelul 2) - componentele de bază ale noului vârf x 00(componente non-de bază x 1 = 0, x 6 = 0,).

Așa cum arată tabelul 2, noua soluție de bază x 00 = (0,10,30,20,40,0) non-optim (linia zero are un scor non-negativ de 7). Prin urmare, cu elementul pivot 1 (a se vedea tabelul 2), construim un nou tabel simplex, adică construirea unei noi soluții de bază fezabile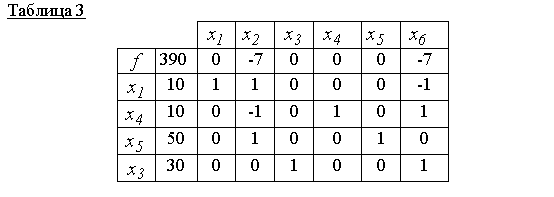

Tabelul 3 corespunde soluției de bază admisibile x 000 = (10,0,30,10,50,0)și este optim pentru că nu există evaluări pozitive în linia zero. prin urmare f (x 000) = 390 este valoarea minimă a funcției obiective.
Răspuns: x 000 = (10, 0, 30, 10, 50, 0)- punctul minim, f (x 000) = 390.

Problemă de programare liniară condiționată standard

Trebuie să finalizați următoarele sarcini în ordinea listată.

Găsiți planul optim pentru problema directă:
a) metoda grafică;
b) metoda simplex (se recomandă utilizarea metodei bazei artificiale pentru a construi planul de referință inițial).
Construiește o dublă problemă.
Găsiți planul optim al problemei duale din soluția grafică a liniei folosind condițiile complementare de slăbire.
Găsiți planul optim pentru problema duală prin prima teoremă a dualității, utilizând tabelul final simplex obținut prin rezolvarea problemei directe (a se vedea itemul 1b). Verificați afirmația „valorile funcțiilor obiective ale unei perechi de probleme duale coincid cu soluțiile lor optime”.
Rezolvați problema duală prin metoda simplex, apoi, folosind tabelul final simplex al problemei duale, găsiți planul optim al problemei directe în conformitate cu prima teoremă a dualității. Comparați rezultatul cu rezultatul obținut prin metoda grafică (a se vedea articolul 1a).
Găsiți soluția integrală optimă:
a) metoda grafică;
b) Prin metoda Gomori.
Comparați valorile funcțiilor soluțiilor întregi și non-întregi

Întrebări pentru autocontrol

Cum este construită o masă simplex?
Cum se reflectă schimbarea de bază în tabel?
Formulați un criteriu de oprire pentru metoda simplex.
Cum se organizează recalcularea tabelelor?
Cu ce rând este convenabil să începeți să recalculați tabelul?

Pentru a permite aplicației să ruleze pe computer, trebuie să faceți următoarele - faceți clic pe Start> Panou de control> Programe> Java. În fereastra Panoului de control Java, selectați fila Securitate, faceți clic pe butonul Editați lista site-urilor, pe butonul Adăugați și introduceți calea către această pagină din bara de adrese a browserului în câmpul liber. Apoi apăsăm butoanele OK, după care repornim computerul.

Pentru a lansa applet-ul, faceți clic pe butonul „Simplex”. Dacă butonul „Simplex” nu este vizibil deasupra acestei linii, atunci Java nu este instalat pe computer.

După ce faceți clic pe butonul „Simplex”, se afișează prima fereastră pentru introducerea numărului de variabile și a numărului de restricții de sarcini pentru metoda simplex.

După ce faceți clic pe butonul „ok”, se afișează o fereastră pentru introducerea datelor rămase ale problemei pentru metoda simplex: modul de afișare (fracții zecimale sau fracții obișnuite), tipul criteriului problemei min sau max, introducerea obiectivului coeficienții funcției și coeficienții sistemului de constrângere cu semnele "≤", "≥" sau "=", restricțiile de forma х i ≥ 0 nu trebuie introduse, le ia în considerare în algoritmul său.

După ce faceți clic pe butonul „Rezolvați”, o fereastră cu rezultatele rezolvării problemei este activată .Fereastra este formată din două părți, în partea superioară există un câmp de text care conține o descriere a reducerii problemei inițiale la forma canonică, care este utilizată pentru a compune primul tabel simplex. În partea de jos a ferestrei, într-un panou cu file, există tabele simplex ale fiecărei iterații cu o mică casetă de text în partea de jos care indică coloana de rezoluție, liniile de rezoluție și alte informații, făcând programul un tutorial. În fila cu tabelul optim (ultimul), soluția optimă obținută la problemă este afișată în câmpul de text.

Vă rugăm să trimiteți orice erori și comentarii observate pe applet la [e-mail protejat] sau sunați la 8 962 700 77 06, pentru care vă vom fi foarte recunoscători.

Programul metodei M

Programul pentru rezolvarea problemei de transport

Iată o soluție manuală (nu un applet) a două probleme folosind o metodă simplex (similară cu o soluție de applet) cu explicații detaliate pentru a înțelege algoritmul de rezolvare a problemelor. Prima problemă conține doar semne de inegalitate "≤" (o problemă cu o bază inițială), a doua poate conține semne "≥", "≤" sau "=" (o problemă cu o bază artificială), sunt rezolvate în moduri diferite .

Metoda Simplex, rezolvarea unei probleme cu o bază inițială

1)Metoda Simplex pentru o problemă cu o bază inițială (toate semnele constrângerilor de inegalitate „≤”).

Să scriem sarcina în canonic formă, adică constrângerile inegalității pot fi rescrise ca egalități prin adăugare bilanț variabile:

Acest sistem este un sistem cu o bază (baza s 1, s 2, s 3, fiecare dintre ele este inclusă într-o singură ecuație a sistemului cu coeficientul 1), x 1 și x 2 sunt variabile libere. Problemele care sunt rezolvate folosind metoda simplex trebuie să aibă următoarele două proprietăți:
- sistemul de constrângeri trebuie să fie un sistem de ecuații cu o bază;
- termenii liberi ai tuturor ecuațiilor din sistem trebuie să fie negativi.

Sistemul rezultat este un sistem cu o bază și termenii săi liberi nu sunt negativi; prin urmare, metoda simplex poate fi aplicată. Să alcătuim primul tabel simplex (Iterarea 0), adică un tabel al coeficienților funcției obiective și un sistem de ecuații pentru variabilele corespunzătoare. Aici "BP" înseamnă coloana variabilelor de bază, "Soluție" - coloana din partea dreaptă a ecuațiilor sistemului. Soluția nu este optimă pentru că există coeficienți negativi în rândul z.

iterația 0

BP	Decizie	Atitudine

Pentru a îmbunătăți soluția, mergeți la următoarea iterație, obțineți următorul tabel simplex. Pentru a face acest lucru, trebuie să alegeți coloana permisivă, adică o variabilă care va fi inclusă în bază la următoarea iterație. Este selectat de cel mai mare coeficient negativ în valoare absolută în rândul z (în problema maximă) - în iterația inițială, aceasta este coloana x 2 (coeficient -6).

Este apoi selectat șir permisiv, adică variabila care va ieși din bază la următoarea iterație. Este selectat de cel mai mic raport dintre coloana „Decizie” și elementele pozitive corespunzătoare ale coloanei de rezolvare (coloana „Raport”) - în iterația inițială, acesta este rândul s 3 (coeficientul 20).

Element permisiv este la intersecția coloanei de rezolvare și a rândului de rezolvare, celula sa este evidențiată, este egală cu 1. Prin urmare, la următoarea iterație, variabila x 2 va înlocui s 3 în bază. Rețineți că relația nu este căutată în linia z; o liniuță "-" este pusă acolo. Dacă există relații minime identice, atunci se alege oricare dintre ele. Dacă în coloana de rezolvare toți coeficienții sunt mai mici sau egali cu 0, atunci soluția problemei este infinită.

1) Calculul rândului x 2 al tabelului "Iterarea 1". În primul rând, împărțim toți membrii rândului de rezolvare s 3 al tabelului "Iterarea 0" la elementul de rezolvare (este egal cu 1 în acest caz) din acest tabel, obținem rândul x 2 în tabelul Iterarea 1. pentru că elementul de rezolvare în acest caz este egal cu 1, apoi rândul s 3 al tabelului "Iterarea 0" va coincide cu rândul x 2 al tabelului "Iterarea 1". Am obținut rândul x 2 al tabelului "Iterarea 1" 0 1 0 0 1 20, restul rândurilor tabelului "Iterarea 1" vor fi obținute din acest rând și rândurile tabelului "Iterarea 0" după cum urmează:

2) Calculul rândului z al tabelului "Iterarea 1". În locul lui -6 în primul rând (rândul z) din coloana x 2 a tabelului Iteration 0, ar trebui să existe 0 în primul rând al tabelului Iteration 1. Pentru a face acest lucru, înmulțim toate elementele rândului x 2 din tabelul „Iterare 1” 0 1 0 0 1 20 cu 6, obținem 0 6 0 0 6 120 și adăugăm acest rând cu primul rând (z - rând) de tabelul „Iterare 0” -4 -6 0 0 0 0, obținem -4 0 0 0 6 120. Zero 0 a apărut în coloana x 2, obiectivul a fost atins. Elementele permisive ale coloanei x 2 sunt evidențiate cu roșu.

3) Calculul rândului s 1 al tabelului "Iterarea 1". În locul 1 din rândul 1 al tabelului "Iterare 0", trebuie să existe 0 în tabelul "Iterare 1". Pentru a face acest lucru, înmulțim toate elementele rândului x 2 din tabelul "Iterare 1" 0 1 0 0 1 20 cu -1, obținem 0 -1 0 0 -1 -20 și adăugăm acest rând cu s 1 - rândul tabelului "Iterare 0" 2 1 1 0 0 64, obținem rândul 2 0 1 0 -1 44. În coloana x 2 obținem 0 necesar.

4) Calculul rândului 2 al tabelului "Iterarea 1". În locul 3 din rândul 2 al tabelului "Iterare 0", trebuie să fie 0 în tabelul "Iterare 1". Pentru a face acest lucru, înmulțim toate elementele rândului x 2 din tabelul "Iterare 1" 0 1 0 0 1 20 cu -3, obținem 0 -3 0 0 -3 -60 și adăugăm acest rând cu s 2 - rândul tabelului "Iterare 0" 1 3 0 1 0 72, obținem rândul 1 0 0 1 -3 12. În coloana x 2, se obține 0. Coloana x 2 din tabelul "Iterarea 1" are devine unul, conține unul 1 și restul 0.

Rândurile din tabelul „Iterarea 1” se obțin conform următoarei reguli:

Rând Nou = Rând Vechi - (Factor Coloană Rezoluție Rând Vechi) * (Rând Nou Rezoluție).

De exemplu, pentru un șir z avem:

Șir de z vechi (-4 -6 0 0 0 0)
- (- 6) * Șir de rezoluție nouă - (0-6 0 0 -6 -120)
= Nouă linie z(-4 0 0 0 6 120) .

Pentru următoarele tabele, recalcularea elementelor de tabel se face în același mod, așa că o omitem.

iterație 1

						Decizie	Atitudine

Iterația 2

						Decizie	Atitudine

Coloana de rezolvare s 3, rândul de rezolvare s 1, s 1 părăsește baza, s 3 intră în bază.

Iterarea 3

						Decizie	Atitudine

În rândul z, toți coeficienții sunt negativi, prin urmare, soluția optimă se obține x 1 = 24, x 2 = 16, z max = 192.

Metoda Simplex, rezolvarea unei probleme cu o bază artificială

2) Să rezolvăm problema cu o bază artificială (cel puțin un semn de constrângeri de inegalitate "≥" sau "=").

Să scriem problema în formă canonică (sub forma unui sistem de ecuații, care necesită metoda simplex), pentru aceasta introducem două variabile x 3 ≥ 0 și x 4 ≥ 0 obținem:

Sistemul de constrângeri oferă o singură variabilă de bază admisibilă x 4, doar că este inclusă într-o singură ecuație în a treia cu un coeficient de 1, așa că adăugăm variabile artificiale R 1 ≥ 0 și R 2 ≥ 0 la prima și a doua ecuații ecuațiile-constrângeri trebuie să fie un sistem cu o bază, adică în fiecare ecuație trebuie să existe o variabilă cu un coeficient de 1, care este inclusă într-o singură ecuație a sistemului, în cazul nostru este R 1, R 2 și x 4. Avem așa-numita problemă M:

Acest sistem este un sistem cu o bază în care R 1, R 2 și x 4 sunt variabile de bază, iar x 1, x 2 și x 3 sunt variabile libere, termenii liberi ai tuturor ecuațiilor sunt negativi. Prin urmare, metoda simplex poate fi utilizată pentru a rezolva problema. Să notăm tabelul inițial simplex:

iterația 0

	Decizie	Atitudine
-16

S-a adăugat linia „Evaluare” la tabel pentru sarcini cu o bază artificială. Se obține prin însumarea coeficienților corespunzători ai rândurilor cu variabilele artificiale (R) cu semnul opus. Va fi prezent în tabel atâta timp cât cel puțin una dintre variabilele artificiale stă la bază. Prin cel mai mare coeficient modulo negativ al rândului „Scor”, coloana de rezolvare este determinată în timp ce se află în tabel. Când rândul „Scor” părăsește tabelul (nu există variabile artificiale în bază), coloana de rezolvare va fi determinată de rândul z, ca în problema cu baza inițială. În acest tabel, coloana de rezolvare este x 2, este selectată în funcție de cea mai mare estimare modulo negativă (-7). Rândul de rezolvare R 2 este selectat în funcție de cel mai mic raport dintre coloana „Decizie” și elementele pozitive corespunzătoare ale coloanei de rezolvare, ca în problema fără variabile artificiale. Aceasta înseamnă că la următoarea iterație variabila x 2 va trece de la liber la bază și variabila R 2 de la bază la liber. Să scriem următorul tabel simplex:

Coloana permisivă x 1, rândul permisiv R 1, R 1 este în afara bazei, x 1 este inclus în bază. După aceea, nu mai există variabile artificiale rămase în bază, deci nu există nicio linie „Evaluare” în următorul tabel:

iterația 2

							Decizie	Atitudine

Apoi, coloana de rezolvare este selectată de rândul z. În rândul z, toți coeficienții sunt negativi, cu excepția coeficientului manechinului R 1, care nu afectează optimitatea atunci când manechinul este în afara bazei. Prin urmare, se obține o soluție optimă x 1 = 6/5; x 2 = 3/5; z max = 72/5.

Cazuri speciale ale metodei Simplex

1) Când o linie dreaptă (dacă este luată în considerare o problemă de programare liniară bidimensională și, în general, un hiperplan) care reprezintă funcția obiectivă este paralelă cu linia dreaptă (hiperplan) corespunzătoare uneia dintre constrângerile de inegalitate (care este satisfăcută la punctul optim ca o egalitate exactă), funcția obiectivă ia una și este, de asemenea, valoarea optimă pe un set de puncte ale limitei regiunii soluțiilor fezabile. Aceste soluții sunt numite soluții optime alternative... Prezența soluțiilor alternative poate fi determinată de tabelul simplex optim. Dacă rândul z al tabelului optim conține zero coeficienți ai variabilelor care nu sunt de bază, atunci există soluții alternative.

2) Dacă în coloana de rezolvare a tabelului simplex toți coeficienții sunt mai mici sau egali cu zero, atunci rândul de rezolvare nu poate fi selectat, în acest caz soluția este nelimitată.

3) Dacă constrângerile unei probleme de programare liniară sunt inconsistente (adică nu pot fi executate simultan), atunci problema nu are soluții fezabile. Această situație nu poate apărea dacă toate inegalitățile care alcătuiesc sistemul de constrângeri sunt de tip "≤" cu laturi non-negative din dreapta, deoarece în acest caz, variabile suplimentare pot constitui o soluție fezabilă. Pentru alte tipuri de constrângeri, se utilizează variabile artificiale. Dacă problema are o soluție, atunci în tabelul optim din bază nu există variabile artificiale (R i). Dacă sunt acolo, atunci problema nu are soluții.